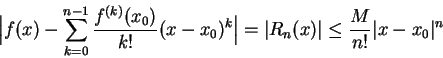泰勒展開的誤差項
首先,讓我們忽略一些細節而直接回顧泰勒多項式 + 誤差項的型式:
這一節就是要談誤差項
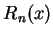 的一種型式。
這種型式通常稱為 微分型式 或拉格朗日 (Lagrange) 型式。
它來自於微分均值定理。
很明顯地,
的一種型式。
這種型式通常稱為 微分型式 或拉格朗日 (Lagrange) 型式。
它來自於微分均值定理。
很明顯地,
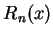 應該是 x 的函數,而且
應該是 x 的函數,而且
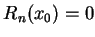 。
此外,我們將以上的 n-1 階泰勒多項式記做
。
此外,我們將以上的 n-1 階泰勒多項式記做
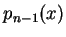 ,
因此
,
因此
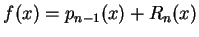 。
。
讓我們再看看微分均值定理說了什麼?
如果 f(x) 是一個在 [a,b] 區間中的 C1 函數,記做
將上述等式重新整理,便得到
您看,這不就是 n = 1 情況下的泰勒多項式和誤差項嗎?
從這裡,我們發現
現在,我們用一套「型式化」推理 (formal reasoning),
來探討一般的正整數 n 情況下
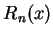 是什麼。所謂「型式化」推理,就是型式上正確但是骨子裡並不完全正確的意思
(但是它推理的結果是正確的)。
型式化的推理,雖然嚴格來說並不正確,但是比較容易讓我們瞭解整個理論架構。
要把它完全寫對,並非十分困難,只是麻煩些,
我們並不打算在這裡講解嚴格而完全正確的推理過程。
是什麼。所謂「型式化」推理,就是型式上正確但是骨子裡並不完全正確的意思
(但是它推理的結果是正確的)。
型式化的推理,雖然嚴格來說並不正確,但是比較容易讓我們瞭解整個理論架構。
要把它完全寫對,並非十分困難,只是麻煩些,
我們並不打算在這裡講解嚴格而完全正確的推理過程。
假設
![$f(x)\in C^n([x_0-R, x_0+R])$](img16.gif) 。
意思是說,f(x) 在 [x0-R, x0+R] 中連續,
而且它在 (x0-R, x0+R) 中的一次、二次、...、n 次導函數
。
意思是說,f(x) 在 [x0-R, x0+R] 中連續,
而且它在 (x0-R, x0+R) 中的一次、二次、...、n 次導函數
都存在,而且都可以拓展成 [x0-R, x0+R] 上的連續函數。
既然
![$f(x)\in C^n([x_0-R, x_0+R])$](img16.gif) 則
則
![$f^{(n-1)}(x)\in C^1([x_0-R, x_0+R])$](img18.gif) 我們可以把微分均值定理應用在它身上,得到:
對任意一個點
我們可以把微分均值定理應用在它身上,得到:
對任意一個點
![$x\in[x_0-R, x_0+R]$](img11.gif) 都有,
都有,
因為
所以,從
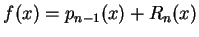 得知
得知
代入前三條式子,我們得知
現在,讓我們假設
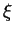 是一個常數,因此與 x 無關
(這裡就是「型式化」推理的錯誤所在,其實
是一個常數,因此與 x 無關
(這裡就是「型式化」推理的錯誤所在,其實
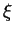 是與 x 有關的,當 x 改變,
是與 x 有關的,當 x 改變,
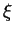 也會變。但是,我們暫且忽略這個事實,繼續做型式化的推理)。則
也會變。但是,我們暫且忽略這個事實,繼續做型式化的推理)。則
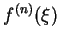 也是一個常數。所以當我們在上式之兩側都做積函數,則是
也是一個常數。所以當我們在上式之兩側都做積函數,則是
積出來
讀者應該可以自行推導以下等式:
代回前一條式子,就獲得
重複在等式兩側做積函數,就得到
這樣,就得到了微分型式的泰勒展開誤差項。
我們結論如下。
如果存在某數 x0 和某正數 R,使得
![$f(x)\in C^n([x_0-R, x_0+R])$](img16.gif) 則對任何
則對任何
![$x\in[x_0-R, x_0+R]$](img11.gif) ,
f(x) 以 x0 為參考點的 n-1 階泰勒多項式與其誤差項就是
,
f(x) 以 x0 為參考點的 n-1 階泰勒多項式與其誤差項就是
雖然我們不能確定
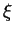 到底是誰,但是如果可以肯定有一個正數 M 使得
到底是誰,但是如果可以肯定有一個正數 M 使得
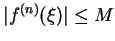 則對於任何介於 x 和 x0 之間的
則對於任何介於 x 和 x0 之間的
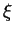 ,
都可以估計泰勒多項式和函數之間的差異,最多也不過是
,
都可以估計泰勒多項式和函數之間的差異,最多也不過是
當 f(x) 無限多次可微,而它的泰勒多項式之階數趨向無限大之後,
就是泰勒級數。如果對某個實數 x
則在那個 x 處的泰勒級數收斂到原函數 f(x)。
現在,我們可以證明正弦函數 sin(x) 以 0 為參考點的泰勒級數對任何實數
x 都收斂。
因為,對於 sin(x) 以 0 為參考點的泰勒多項式誤差項而言,
所以
因為
此時 |x| 是某個已經選定的實數,但是 n 卻越來越大,可見
只是,如果 |x| 越大,需要的階數 n 就越高,
才能獲得較小的誤差。不過,對於正弦函數而言,
我們只需要討論 x 在
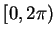 或者
或者
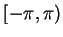 之內,所以上述問題並不嚴重。
之內,所以上述問題並不嚴重。
以下習題常說「有效數字」,意思是說從第一個非零數字以後的數。
例如 3002, 1.234, 0.002709, 0.00006667 都有四位有效數字。
習題
- 請用 ln(x) 以 1 為參考點的 4 階泰勒多項式計算 ln(1.5) 的估計值,
並寫出此估計值的誤差最多是多少。
如果需要數值計算,寫出四位有效數字。
- 請用 sin(x) 以 0 為參考點的 5 階泰勒多項式計算 sin(1) 的估計值,
並寫出此估計值的誤差最多是多少。
如果需要數值計算,寫出四位有效數字。
- 請用
Created: Aug 16, 2001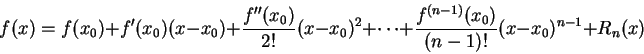
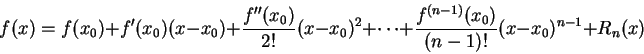
![]() 是什麼。所謂「型式化」推理,就是型式上正確但是骨子裡並不完全正確的意思
(但是它推理的結果是正確的)。
型式化的推理,雖然嚴格來說並不正確,但是比較容易讓我們瞭解整個理論架構。
要把它完全寫對,並非十分困難,只是麻煩些,
我們並不打算在這裡講解嚴格而完全正確的推理過程。
是什麼。所謂「型式化」推理,就是型式上正確但是骨子裡並不完全正確的意思
(但是它推理的結果是正確的)。
型式化的推理,雖然嚴格來說並不正確,但是比較容易讓我們瞭解整個理論架構。
要把它完全寫對,並非十分困難,只是麻煩些,
我們並不打算在這裡講解嚴格而完全正確的推理過程。
![]() 。
意思是說,f(x) 在 [x0-R, x0+R] 中連續,
而且它在 (x0-R, x0+R) 中的一次、二次、...、n 次導函數
。
意思是說,f(x) 在 [x0-R, x0+R] 中連續,
而且它在 (x0-R, x0+R) 中的一次、二次、...、n 次導函數
![]() 則
則
![]() 我們可以把微分均值定理應用在它身上,得到:
對任意一個點
我們可以把微分均值定理應用在它身上,得到:
對任意一個點
![]() 都有,
都有,
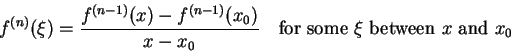
![]() 是一個常數,因此與 x 無關
(這裡就是「型式化」推理的錯誤所在,其實
是一個常數,因此與 x 無關
(這裡就是「型式化」推理的錯誤所在,其實
![]() 是與 x 有關的,當 x 改變,
是與 x 有關的,當 x 改變,
![]() 也會變。但是,我們暫且忽略這個事實,繼續做型式化的推理)。則
也會變。但是,我們暫且忽略這個事實,繼續做型式化的推理)。則
![]() 也是一個常數。所以當我們在上式之兩側都做積函數,則是
也是一個常數。所以當我們在上式之兩側都做積函數,則是
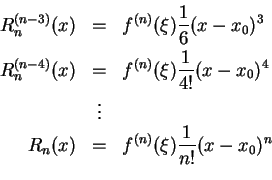
則對任何
, f(x) 以 x0 為參考點的 n-1 階泰勒多項式與其誤差項就是
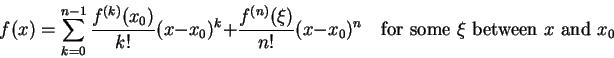
![]() 到底是誰,但是如果可以肯定有一個正數 M 使得
到底是誰,但是如果可以肯定有一個正數 M 使得
![]() 則對於任何介於 x 和 x0 之間的
則對於任何介於 x 和 x0 之間的
![]() ,
都可以估計泰勒多項式和函數之間的差異,最多也不過是
,
都可以估計泰勒多項式和函數之間的差異,最多也不過是