切片方法求體積
這一份教材應該要畫許多圖來做視覺輔助,
但是這些圖都不是普通的測繪 (plot) 可以勝任,
必須要做些視覺處理。我們現在沒時間 (也沒經費) 畫這些圖,
只好請讀者充分發揮想像力了。
我們先舉一個很簡單的例子,從這個例子裡,我們學習一種立積分式子的方法。
讓我們來推導圓柱體的體積公式。
假設一個圓柱體的底部半徑為 r (r > 0) 而高為 h (h > 0)。
我們設定一個三維 (x-y-z) 坐標系統,讓圓柱體的底部就在 x-y 平面上,
而底部的圓心在坐標系統的原點。圓柱的中心軸就是 z 軸,
而圓柱的頂部就在 z=h 處。
我們都知道,這樣的圓柱體積是
現在,我們將 z 軸的 [0,h] 區間等分成 n 段,令 zk 是分割節點,
而每一段的寬度是
從以上的例子,我們看到一個通則:如果要求體積,
可以將它切成一片一片的薄片,再將所有薄片的體積加起來。
為了能使用微積分作為求體積的工具,
我們必須給定一個坐標系統,並且設法將這個體積的外圍寫成方程式。
然後,切成薄片個過程,就對應一種閉區間內的分割。
而薄片體積的和,就變成一種黎曼和。將
就得到一個定積分式子,然後求那個定積分就行了。
我們可以正經八百地按照規矩來:先寫出黎曼和,再取極限改寫成定積分。
也可以利用一種「型式化」的思維方法,那就是,把每一個點 x 的長度
(或寬度、或厚度) 假定為 dx (或者是 y 的長度就是 dy、
z 的長度就是 dz...,它們只不過是自變量的名字,可以換成任何名字),
然後對於 [a,b] 區間中的每一個點 x,做一個厚度 (或長度、或寬度、或深度...)
為 dx 的薄片。那麼,這片薄片的體積就含有一個 dx。
對每一個 x 就有一張薄片,所以有無窮多張薄片。
把這無窮多張薄片的體積加起來的動作,就不再是
而直接寫
。
回到前面的圓柱體例子。
對於 [0,h] 區間中的每一個 z 都切一張薄片。
這張薄片的面積是
而它的厚度是 dz,所以薄片的體積是
那麼,整個圓柱的體積就是
正式的步驟,應該要先建立黎曼和,然後轉換成積分型式。
但是如果讀者可以在直覺上接受上述「厚度為 dz」的「型式化」推理方法,
其實事情會變得簡單得多。
對於某些問題,每張薄片的體積可能會出現 dx 和 (dx)2 或者更高次方。
但是因為 dx 本身已經非常非常小了 (以前稱之為 無限小量 (infinitesimal),
近代不流行這個名詞了),所以 (dx)2 就更小而可以忽略不計。
讓我們利用上述「型式化」推理方法,來推導球的體積。
假設一個半徑為 r (r > 0) 的球,放在 x-y-z 坐標系統中,
其圓心就在原點。因為對稱性,我們只需要計算上半球的體積,然後再乘以二就行了。
假設我們沿著 z 軸做橫切片,則 z 的範圍是在 [0,r] 之內。
我相信讀者都有足夠的幾何知識,而且有本領知道,
每一張薄片都是圓形,其半徑是
而厚度是 dz,所以薄片體積是
現在,可以立下球體積的積分式為
我們留給讀者自己去驗證,上述積分值是
。
許多有對稱性的體積,可以經由面積的旋轉而得到。
譬如半徑為 r 的上半球,可以是 x-y 坐標平面上以 r 為半徑的四分圓旋轉而成。
比較詳細地說明,則先考慮
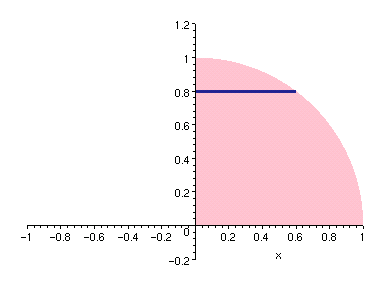 這段曲線,以它和 x 軸、y 軸圍成一塊區域,稱之為四分圓。
參照右圖。
將四分圓繞 y 軸旋轉 360 度 (一圈)、不就是上半球嗎?
目前無法製作動畫,但是讀者應該可以自行想像這個動作。
如果對 y 切片,則每一片是以四分圓內一個線段旋轉而成的圓。
參照右圖,其半徑為線段長度,也就是
,
厚度為 dy。因此,立下積分式:
這段曲線,以它和 x 軸、y 軸圍成一塊區域,稱之為四分圓。
參照右圖。
將四分圓繞 y 軸旋轉 360 度 (一圈)、不就是上半球嗎?
目前無法製作動畫,但是讀者應該可以自行想像這個動作。
如果對 y 切片,則每一片是以四分圓內一個線段旋轉而成的圓。
參照右圖,其半徑為線段長度,也就是
,
厚度為 dy。因此,立下積分式:
也就是上半球的體積。
如果您懷疑 z 軸去了哪裡,其實這不重要,不過您如果一定要問,
可以想像 z 軸就是通過原點、垂直於 x-y 平面、朝著您自己的方向而來的直線。
以上述「旋轉體」的想法,我們示範圓錐體的體積公式。
一個高為 h (h > 0) 而底部半徑為 r (r > 0) 的圓錐體,
可以想像是一個三角形的旋轉體。
在 x-y 平面上以
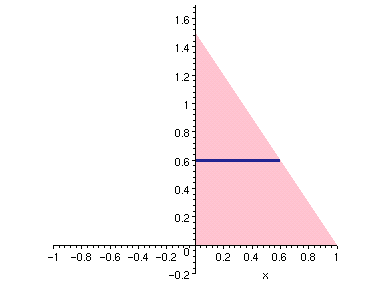 三點畫出一個三角形,將此三角形繞 y 軸旋轉一圈,就是上述圓錐體。
參照右圖。
現在,我們沿著 y 軸切片 (也就是平行於 x 軸切片)。
因為是旋轉體,所以每一片是一個圓,
其厚度為 dy 而半徑為 y 到三角形斜邊的水平距離 (右圖中藍色線段的長度)。
斜邊直線的方程式是
三點畫出一個三角形,將此三角形繞 y 軸旋轉一圈,就是上述圓錐體。
參照右圖。
現在,我們沿著 y 軸切片 (也就是平行於 x 軸切片)。
因為是旋轉體,所以每一片是一個圓,
其厚度為 dy 而半徑為 y 到三角形斜邊的水平距離 (右圖中藍色線段的長度)。
斜邊直線的方程式是
因此
就是在 y 點切片出來的半徑。現在,可以立下圓錐體的積分式:
習題
- 埃及金字塔大約是一個方尖錐:它的每一片水平截面都是正方形。
古夫王金字塔的底部邊長大約是 230 公尺,高度大約 125 公尺,
請問此金字塔的體積大約是多少立方公尺?[HH]
- 計算 y = e-x 在 [0,1] 之間與 x 軸、y 軸圍成的區域,
繞 x 軸旋轉一圈所造成的體積。
- 計算 y = e-x 在 [0,1] 之間與 x 軸、y 軸圍成的區域,
繞 y 軸旋轉一圈所造成的體積。
- 計算 y = x 和 y = x2 所圍成的區域,
繞水平線 y=3 旋轉一圈所造成的體積。[HH]
Created: Aug 16, 2001 三點畫出一個三角形,將此三角形繞 y 軸旋轉一圈,就是上述圓錐體。
參照右圖。
現在,我們沿著 y 軸切片 (也就是平行於 x 軸切片)。
因為是旋轉體,所以每一片是一個圓,
其厚度為 dy 而半徑為 y 到三角形斜邊的水平距離 (右圖中藍色線段的長度)。
斜邊直線的方程式是
三點畫出一個三角形,將此三角形繞 y 軸旋轉一圈,就是上述圓錐體。
參照右圖。
現在,我們沿著 y 軸切片 (也就是平行於 x 軸切片)。
因為是旋轉體,所以每一片是一個圓,
其厚度為 dy 而半徑為 y 到三角形斜邊的水平距離 (右圖中藍色線段的長度)。
斜邊直線的方程式是
 這段曲線,以它和 x 軸、y 軸圍成一塊區域,稱之為四分圓。
參照右圖。
將四分圓繞 y 軸旋轉 360 度 (一圈)、不就是上半球嗎?
目前無法製作動畫,但是讀者應該可以自行想像這個動作。
如果對 y 切片,則每一片是以四分圓內一個線段旋轉而成的圓。
參照右圖,其半徑為線段長度,也就是
這段曲線,以它和 x 軸、y 軸圍成一塊區域,稱之為四分圓。
參照右圖。
將四分圓繞 y 軸旋轉 360 度 (一圈)、不就是上半球嗎?
目前無法製作動畫,但是讀者應該可以自行想像這個動作。
如果對 y 切片,則每一片是以四分圓內一個線段旋轉而成的圓。
參照右圖,其半徑為線段長度,也就是