阿基米德求拋物線面積
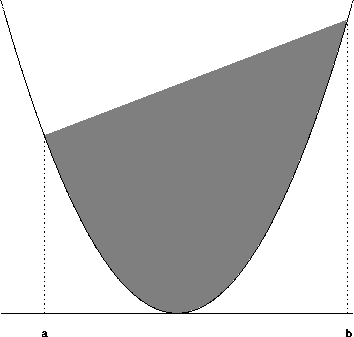
阿基米德欲求拋物線 y=x2 在 [a,b]
區間內,內部圍成的面積,稱為 A。如下圖。
他的想法是,令 c 是 [a,b] 的中點,
考慮由 (a,a2), (b,b2)
和 (c,c2) 所決定的三角形。稱此三角形的面積為
A0 發現此面積可以由三個梯形面積計算出來。
答案是
A0=(b-a)3/8
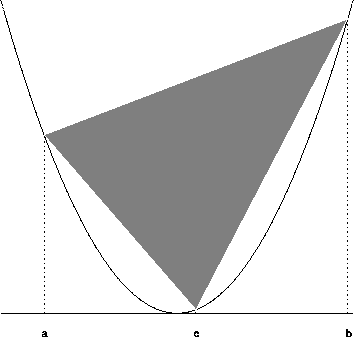
然後,阿基米德在 [a,c] 內取中點 c1
和 [c,b] 內取中點 c2。
依前面的形式取兩個小三角形,令它們的面積是 A1。如下圖。
其實,發現只要利用前面的 A0 公式,代入
c=(b+a)/2 即可得到
A1=(1/4) A0
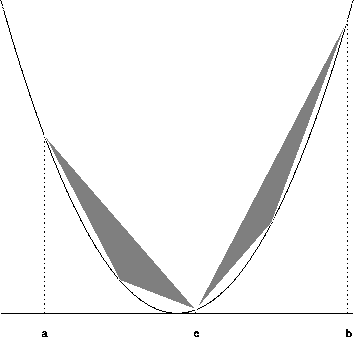
讀者請自行推廣以上論述,定義越來越小的三角形面積 A2,
A3 ... 並且得到
A2 = (1/4) A1
= (1/4)2 A0。
依此類推,得到
An = (1/4)n A0。
觀察
A=A0 + A1+A2
+ ...
故得
A= (1 + (1/4)2 + (1/4)3 + ...) A0
= (4/3) A0 = (b-a)3 /6
用梯形面積減去 A,阿基米德其實也得到了拋物線
y=x2 在 [a,b] 內的曲線下面積。
亦即
(a2+b2)(b-a)/2
- (b-a)3 /6
= (1/3) (b3 - a3)
這其實就是今天的定積分公式。
Created: Nov 14, 1999