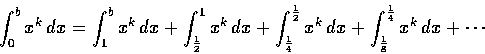費瑪求冪函數積分

令 0<a<b，n 為一非負整數，考慮 y=x^k 在 [a,b] 區間內的曲線下面積。當 k=0 和 k=1 的情況，是簡單的。當 k=2 的情形，在西元前二百多年，阿基米德已經有了公式，或者利用 1+4+9+...+n² 的求和公式，配合黎曼和的定義，也可以求得上述面積問題的公式。後者留給讀者自己嘗試。當 k>=3 的時候，費瑪有一套算法。這是大約 1635 年的事。

費瑪的想法類似以後的黎曼和。他的分割方式並非均勻分割，而是任取一個正整數 n，令

$\begin{displaymath}h = (\frac{b}{a})^{\frac1n} \end{displaymath}$

定義

x₀=a, x₁=ah, x₂=ah², ..., x_n=ahⁿ=b

則 {x₀, x₁, x₂, ..., x_n} 就是 [a,b] 區間內的一個 n 段分割。在這個分割上取其右黎曼和，得到

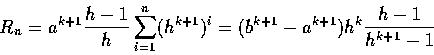
$\begin{displaymath}R_n = a^{k+1} \frac{h-1}h \sum_{i=1}^n (h^{k+1})^i = (b^{k+1} - a^{k+1}) h^k \frac{h-1}{h^{k+1}-1} \end{displaymath}$

當 n -> 無限大的時候，h -> 1。由於

$\begin{displaymath}\frac{h-1}{h^{k+1}-1} = \frac1{h^k + h^{k-1} + \cdots + h + 1} \end{displaymath}$

故

$\begin{displaymath}\lim_{n\to\infty} R_n = \frac1{k+1} (b^{k+1}-a^{k+1}) \end{displaymath}$

這就是我們今天的定積分公式。我們將細節留給讀者去驗證。

其實，仔細檢查前面的思路，我們會發現，k 不必是個正整數，只要 k 不是 -1，它可以是任何數，而上述公式都會成立。

但是前面的結果只對 a>0 的情況有效。但是，針對 [0,b] 區間內的定積分問題，我們可以不失一般性地假設 b>1 而且則上式中的每個積分都有非零的積分下界，因此可以代入前面求得的公式。在將這些積分值加在一起，就會得到

$\begin{displaymath}\int_0^b x^k\,dx = \int_1^b x^k\,dx + \int_{\frac12}^1 x^k\,d... ...{\frac12} x^k\,dx + \int_{\frac18}^{\frac14} x^k\,dx + \cdots \end{displaymath}$

我們也將此細節，和 a<0 的推廣，留給讀者練習。總之，我們看到，費瑪已經得到了我們今天的冪函數定積分公式。只是他沒有進一步去發掘它和導函數運算的關係。