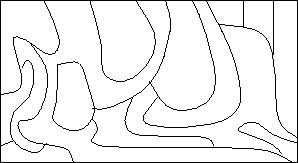
所謂四色問題, 其敘述非常簡單:

根據歷史上知道的記錄, 四色問題首先由英國的 Francis Guthrie 在 1852 提出. 當時他在畫英國各郡的地圖, 而發現了這個現象. 經過許多實驗之後, 他歸納出一個結論, 就是: 最多只需要四種不同顏色, 就可以畫任何地圖. 他將這個心得告訴了他的兄弟: Frederick Guthrie. 後者又請教了當時英國最主要的數學家: deMorgan. 這個問題首次見於文獻, 是在 1878 年, 由 Cayley 所寫.
就在問題傳出去之後, 立刻就有所回響. 在 1879 年 Kempe 發表了一個證明; 1880 年 Tait 也發表了一個證明. 事隔十一年後, 這兩個證明分別被 Heawood 和 Petersen 發現是有錯的. 但是, 兩個錯誤的嘗試都有所貢獻. Kempe 的論述, 其實是證明了所謂的五色定理. 也就是說, 只要五種不同顏色就可以為平面地圖著色. 而 Tait 的論述, 後來用圖論 (graph theory) 的語言寫出來, 變成一個和四色問題等價的圖論問題.
由於前人的失敗, 四色問題更受到注意, 而開始有些主要的數學家投入這個問題. 1902 年秋季, 閔可夫斯基 (Hermann Minkowsky, 1864--1909) 獲得哥丁根 (Gottingen) 的教職 (Hilbert 在那裡, 他們從年輕的時候就是好朋友). 不久, 大概是 1903 春季, 他講授一門拓撲 (topology) 課程. 在課堂上, 他很傲慢地對同學們說, 四色問題之所以還沒有被解決, 乃是因為到目前為止, 只有三流的數學家試過這個問題. 他相信他有一個解法, 而且他要在課堂上當場證明四色問題. 一堂課一堂課地過去了, 始終無法結束. 很快地幾個禮拜過去了, 他還是不能結束他的證明. 有一天早上, 當他踏上講臺那一刻, 天空打了一個大霹靂. 他平靜地對學生說, 一定是老天爺因為他的狂妄自大而發怒了. 然後他承認自己的證明無法成功, 接著就繼續講拓撲的課程.
1913 年, 美國哈佛大學的 Birkhoff 對這個問題做出了一些貢獻. 他的理論使得 Franklin 在 1922 得以證明, 如果地圖上的區域不超過 25 個, 則四色問題的猜想是正確的. 同樣的想法, 被 Heesch 繼續發展, 發現了兩個主要的方法: 所謂的 reducibility 和 discharging. 應用這兩種方法, 數學家可以將四色問題分解成有限多種狀況, 而每種狀況都可以在有限步驟內獲得驗證. 雖然有限, 但是卻非常地多. 像這樣的問題, 當然電腦是可以幫忙的. 的確有人用了電腦, 那就是在伊利諾大學的 Appel, Haken 和 Koch, 他們在 1977 年發表了由電腦輔助的證明, 證明了四色問題猜想的正確性. 這是有史以來第一個電腦輔助證明, 當時引起許多數學家的疑忌.
四色問題並未從此結束. 仍有許多在圖論, 代數, 拓撲, 統計力學等領域中的研究者, 仍在研究這個問題所衍生出來的新問題, 或是利用它來解決其他領域的問題.