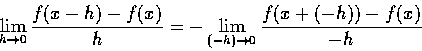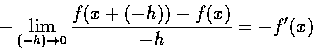導數的數學定義
利用極限所下的導數定義。若 f(x) 是一個函數,
x0 是定義域中的一個數,若以下極限存在
則稱 f(x) 在 x0 處可微 (differentiable),
微分 (differentiation) 的結果稱為導數 (derivative),
記作
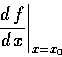
或
f ' (
x0)
如果 f(x) 在 (a,b) 中的每個點 x 都可微,
則定義一個從 (a,b) 對應到 f(x) 的導數的新函數,
這個函數叫做 f(x) 的導函數,記作
f ' (x)
如果可以利用公式與微分運算規則,找到 f ' (x),
那麼只要在這個函數中代入一個 x 的數值,就可以得到 f(x)
的導數。
數學定義有什麼用處?根據我們對極限的知識,可以做以下幾種應用。
- 拿來推導基本函數的導函數公式
- 例如常數函數和冪函數 xn (n 是正整數)
的導函數公式。
以後還會推導更多的導函數公式。
- 拿來推導微分運算規則
- 例如線性性質 (兩個性質),因此可做多項式的導函數。
例如函數脹縮:令 g(x)=f(ax),
則 g ' (x) = a f ' (ax),
這是 chain rule 的一個特例,但可以先知道,
並應用到以角度為單位的三角函數導數計算。
- 拿來證明一些關於導數的定理
- 例如證明偶函數的導函數若存在則必為奇函數。
若 f(x) 是一個偶函數,則已知
f(-x)=f(x)。
根據導數的定義
我們將 x 的位置代入 -x,得到
由偶函數性質得到
但是右式不能直接拿來當做導數,必須在形式上做些處理:
這是因為如果 h 趨近於 0,當然 -h 也趨近於 0。
這時才能根據導數的定義而得到
故得證。
Created: Apr 16, 1997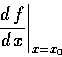 或 f ' (x0)
或 f ' (x0)