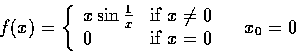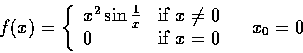導數的數值估計
若一個函數 f(x) 在某點 x0 可微,
則根據定義知道
將左右兩式取平均,得到
若我們已經透過圖形的觀察或理論推演,知道 f(x)
極可能在 x0 處可微,則可以用上式來計算導數
的估計值。
如果事先不知道是否可微,則要小心上面的算法。
例如當 f(x) 是偶函數時,不管它在 0 處是否可微,
上面的那個分數永遠是 0。看下面的第 4 個例子。
若無法從圖形或理論上判斷,而必須以數值估計,
則必須以高精度的數值計算,分別用越來越小的正數 h
分別去計算以上第一個式子中兩邊的極限。
若其數值有越來越多的位數相同,則上面的極限就非常可能存在,
而那些不變動的數字部分,就幾乎是極限。
如果兩邊的極限都可能存在,而且彼此相等,
則 f(x) 極可能在 x0 處可微。
否則,f(x) 極可能在 x0 處不可微。
我們用以下五個例子來實驗:
-
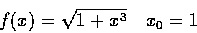
- f(x) = sin x, x0 = 0
- f(x) = 2x, x0 = 0
-
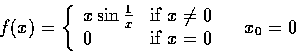
-
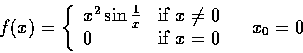
以下是提供實驗的 Maple Worksheet。您必須有 Maple 程式才能開啟。
Created: Apr 16, 1997