有說利用日常生活情境作為學習的出發點,可以提高學習興趣,促進學習效果, 這一點看似成立 (不少「目標為本課程」的官方文件都如是說!), 卻又似乎同時暗示了抽空的、抽象的或脫離生活實踐的數學未能刺激學習興趣, 又或無助於知識的學習與運用。 但君不見不少所謂益智的 IQ 題,都是「不切實際」的, 但嘗試解答的人卻情緒高漲並且感到趣味盎然。 可見簡簡單單的這一點看似成立的所謂「常識」也值得大家認真地從正反兩面去想想。 篇幅所限,大問題不談了,只討論一下文字題虛擬的處境的真實性會涉及哪些問題, 又或者從其反面說,完全脫離日常生活實際的數學難題又是否完全不可取呢?
首先,善用日常生活處境作為學習的出發點可以促進學習,幾近常識,爭議不大。 而聯結論 (associationism,或稱 connectionism) 的代表人物之一、 著名的學習心理學家桑代克 (Edward L. Thorndike, 1874-1949) 所著的《算術心理學》 (The Psychology of Arithmetic, 1922) 早已提出算術學習涉及不同的感應結 (bond) 需要通過練習來強化, 而這類練習題若能設計得有趣並近於實際應用則效果更佳 (註 [3])。 雖然如此,我們也必須注意到學生面對實際處境時的反應, 與面對一題數學難題時的反應有所區別。縱使後者可能以前者作為內容, 無容置疑,數學課之中的數學問題與日常應用其實在多方面都有分別。
讓我們先來看看以下這個有趣的報導 (註 [4]): 一位心理學家走到一個 (美國) 貧窮地區進行比奈測驗 (Binet test), 即所謂智商測驗,其中有算術題一道,以考核小孩子的計算能力。 心理學家問小孩:「如果你到雜貨店買糖果,值 6 仙,你付了 10 仙, 應找回零錢多少?」小孩答他從未擁有過 10 仙,如果有, 他絕不會拿來買糖果,況且他媽媽也會做糖果。 心理學家仍想考核小孩能否計算 10 減 6,於是轉一個問題,繼續問小孩: 「如果你父親吩咐你放牛,你帶了 10 頭牛去草場,但其中 6 頭走失了, 你還可以帶多少頭牛回家呢?」 小孩子立刻回答,「我們壓根兒就沒有 10 頭牛,若果有而我又丟失了 6 頭的話, 我那有膽子回家呢!」這個回答似乎反映了小孩子一點兒減數的知識, 但心理學家當然不滿意, 嘗試再這樣問:「如果學校裡有 10 個孩子,其中 6 個因患痳疹沒有上學, 那麼學校還有多少個孩子?」 小孩子很爽快地回應說:「一個也沒有,因為其他的都怕會傳染到痳疹而不上學。」 顯然以上對答非常精采,小孩子的智力應不成問題吧, 但由於將算術題「鑲嵌」在現實的情境中, 心理學家始終不能肯定小孩子能否計算 10-6。 這件趣事其實來自一本三十年代的教育心理學著作, 聽起來並不陌生,或者我們小時候也曾被人問過類似的問題, 諸如樹上有 10 隻小鳥,獵人瞄準了 1 隻並開槍打牠下來,問樹上還有小鳥若干。 如果你正經八百地計算 10 減 1 的話一定讓出題的人笑得人仰馬翻。 但回答問題時,何時才要考慮實際條件,何時可以當成虛假的荒誕數題呢, 其實不簡單呢!
我們又試看另一個事件 (註 [5]):1980 年某天, 在法國 Grenoble 著名的數學教育研究所 Institut de recherche sur l'enseignement des mathematiques (簡稱 IREM) 初等數學教學的一個工作小組內一名成員忽發奇想, 向他們的二、三年級的小學生問這樣一個問題:「船上有綿羊 26 隻、 山羊 10 隻,問船長幾歲?」97 位被問的小孩子中有 76 位, 想用這些數字通過各種運算拼湊而來的數字作答案。 之後,他們在更多學校的班級上重覆這個問題, 並且也附加了另一些類似的問題,結果也差不多; 類似的問題亦曾在中國大陸作過測試,結果亦是意料之內 (註 [6])。 這件趣事早已成為數學教育界津津樂道的笑話之一。 但我們可以肯定地說,若這群小朋友確實置身於這麼一條船上, 看著這麼一群可愛的山羊、綿羊, 絕不會天馬行空地聯想到船長的歲數會與這些牲口的數目有何關係吧 (註 [7])! 由此例子可見,學生自小在數學教室長大,已經習得一些對數學的看法, 這些想法倒過來影響著他們如何學習數學。即如這裡, 小朋友完全相信每一題老師提出的數學問題都有答案, 而且一般只有一個是正確的 (註 [8])。
尤有甚之,德國有人曾經這樣試過 (幾近惡作劇!), 將以下一段文字混入一系列普通的文字題當中作為其中一題 (註 [9]):
羅倫茲先生 (Mr. Lorenz) 與三位同事早上九時由比麗菲德 (Bielefeld) 駕車出發, 走了 360KM 路,到達法蘭克福 (Frankfurt),途中休息 30 分鐘。測驗的對象是幼稚園至六年級的德國小朋友,結果是班級越高, 越多學生嘗試計算,並且得出「答案」。 這裡有趣的是,連問題也沒有提出,學生就已經「自動自覺」地去求解了! 這個結果提醒我們,目前的數學教學方式似乎在鼓勵小孩子將學校的學習和解題, 抽離於現實生活之外,這才是一個我們必須反省的關鍵。
那麼數學課是否真的有些什麼特別,以致學生「懂得」以另外一種方式、 態度來處理數學課涉及的問題呢? 瑞典心理學家 Roger Saljo 以下這個實驗大概可以令你相信確有其事吧 (註 [10])。 他與同事以第八及第九級的學生 (年齡 15 至 16 歲) 作為對象, 分別在數學課和社會公民課中給予當地郵政局的郵費表部分作參考資料, 要求回答一封重 120 克信件的郵費, 以及另外七封重量由 10 克至 1200 克信件的郵費。 結果顯示兩個年級的情況都類似, 就是較多在數學課的學生試圖用比例的方式來計算郵費, 在社會公民課的學生則傾向 (運用在日常生活中正確的方法) 從郵費表直接讀出信件應付的郵費; 不過面對七封不同重量的信件時, 兩群學生都較多利用郵費表直接讀出郵資而不會利用算術計算, 雖然用計算方法的學生人數在數學課的仍較在社會公民課的為多。 這裡我們隱約見到當問題的真實性較高時 (即不單只求一封信的郵費而是較方便地同時找出七封信的郵資), 學生還是會考慮一些現實需要和條件的。 (請注意:這裡若考慮現實的做法,則不必用上比例的計算方式。)
但這個例子明顯地告訴我們, 連一般的生活問題在數學課時提出都會得到學生「另眼相看」, 用數學課中「合法」的方法來處理, 我們便要小心處理所謂數學文字題或課業所虛擬的生活處境, 設題時先弄清楚究竟我們期望學生只當其為一個趣味性的、 假想性的問題情境,卻不必理會現實世界中的習慣做法和限制呢? 還是期望學生懂得利用真實環境中特有的各種可供利用的工具、條件, 或被認可的簡化、略化和折衷呢? 重要的是,我們必須意識到所謂處境、情境等, 並不單單在於涉及的客體和可見的物理條件, 還有一系列不可能窮舉的生活世界 (life-world) 中有關的條件和原則, 諸如細節描述或說明至何種程俐才算恰當、 某個場合或場所人們一般既定的互動模式如何等等, 往往作為共同的生活背景而不自覺,尤如人生活於空氣中那般自然 (註 [11])。 要認真地探討處境認知 (situated cognition,見註 [12]) 以致如何利用情境學習, 不能不回歸至一些相關的哲學框架作適當的反思, 正如先前部分學習心理學研究也得回溯至胡塞爾 (Edmund Husserl)、 海德格 (Martin Heidegger) 和伽達瑪 (Hans-Georg Gadamer) 等的現象學 (phenomenology) 想法 (註 [13]), 又或者以較有哲學深度的活動理論 (activity theory) 作為心理學研究起點 (註 [14])。 在此筆者不打算談得太遠,只想指出有關的學習問題充滿複雜性, 不宜隨便或盲目地約化成一般所謂的「情境學習」。而且頗多時候, 這些所謂的「情境」往往未經深思,還沒有考慮學習者的經驗和角度, 僅是設計者眼中一廂情願的「情境」而矣。
無可否認,能夠有效地將生活中的處境引入教學設計當中, 適當地引導學生利用他們既有的認識作合理的數學化, 可以令學生慢慢建立相關的數學概念和體會數學的思考方法。 有趣的處境難題可以提高學習興趣,加強他們對學習的投入, 從而令學生對相關的知識有較深刻的印象, 亦會得在面對實際問題時學習以數學的眼光來分析, 從而提高他們的數學知識的實用性。這些都是教育工作者期望的好結果, 只是我們也必須注意到上述談過的種種問題, 要認真思考如何避免太多太人工化的虛擬處境, 反會令學生在不經不覺之間「學懂」了: 數學不過是一堆貌似真實卻是堆砌出來的假問題。 一味用脫離現實的方式來理解或用不設實際的方法來求解, 最終失卻了利用處境學習的意義和價值。
筆者知道不少教師在面對「目標為本課程」如何實施時, 都遇到與上述相關的一些問題。 目前既有的「目標為本課程」框架根本不可能合理地看待數學科的特殊性, 要知道數學知識本身的特殊性及抽象性, 絕不是一個所謂「情境化課業」的提法可以有效和合適地處理得到的 (註 [15])。 如果盲目地將每一個數學單元教學都要「處境化」來進行學習, 只怕最終我們一代的學生都變成柏拉圖 (Plato) 那著名的「地穴比諭」 (the simile of the cave) 中那些永遠只能生活在眼見的「現實」假象中的「地穴囚徒」吧 (註 [16])。
其實,數學以其純粹形式出現的很多情境都足以令不少學生傾心而沉醉於解題之中, 而不必一定要借助於所謂現實情境作為添加劑,已能深得數學學習之精粹; 問題反而是數學教師本身的數學素養, 是否足以支撐一個有數學味道的數學課 (註 [17]), 這就涉及到數學教師專業化的問題。 雖然我們不應武斷地認為所有學生都會對這類問題感到特別有趣, 這也許根本就不可能 (即或許根本不存在一套對所有學生同時有良好效果的教材或教法), 但也同時必須認識這樣一個事實, 就是學生群中有著不同的學習動機、興趣、取向和認知風格 (cognitive style), 其中至少有部分學生值得利用這種方式、進路來加以啟發。 讓我們看看以下例子,對於較低年級的學生,將問題說成這樣會多一些趣味:
農夫病得快要死了,他打算將他的田地分給四個兒子, 又咆他們因分配不均而爭吵,所以希望將他的田產 (見右圖) 分成四塊大小冷狀完全一樣的田地, 現在正大傷腦筋。你可以幫幫他解決這臨終最後的一個難題嗎?
但對於較高年級而又已經知道何謂全等圖形 (congruent figures) 的學生, 以純幾何的問題提法亦可能令他們更快地數學化整個問題, 進而探討更多其他不同形狀的切割可能性。 縱使以小學數學內容而論,數字的性質往往足以令小朋友著迷,因數、倍數、質數 (或稱素數)、幻方、與及各種數字運算的規律性,例如:
1/7
= 0.142857… (循環)
2/7
= 0.285714… (循環)
3/7
= 0.428571… (循環)
4/7
= 0.571428… (循環)
5/7
= 0.714285… (循環)
6/7
= 0.857142… (循環)
又例如:
5882352941176470 x 3 = ?
5882352941176470 x 4 = ?
5882352941176470 x 5 = ?
5882352941176470 x 6 = ?
5882352941176470 x 7 = ?
5882352941176470 x 8 = ?
5882352941176470 x 9 = ?
又例如以下兩個圖形由於都以圓形部分為周界,若要計算其面積, 我們起初總會覺得必然涉及 p 的數值。
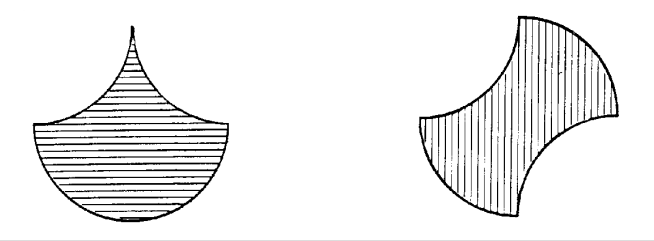
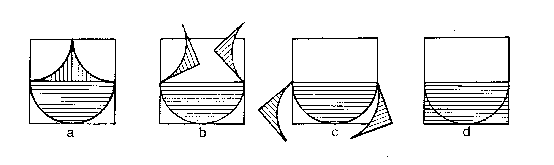
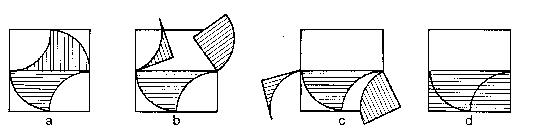
凡此種種都足以成為數學課堂中很好的探討問題, 而不必尋求一個什麼「現實處境」以涵括之 (註 [19])。 即以「費瑪最後定理」 (Fermat's last theorem) 為例, 定理的提法連一般數學水平的公眾也能明白, 而這道難題在過去三百多年不知引起過多少對數學有興趣的人嘗試過 (見註 [20])。 又如尚未被解決的「哥德巴赫猜想 」 (Goldbach conjecture,見註 [21]), 連初懂何謂質數的小學生也能明白,而且對他們已甚具挑戰性。
筆者想藉此文帶出的是希望數學教師還以數學難題本身應有的位置, 請推行「目標為本課程」的教師們, 千萬不要給所有學習設計和數學難題都披上一層「現實生活處境」的外衣, 而應該因應數學課節內容的實質, 以及學生的學習能力、水平、興趣、取向和認知風格來進行合適的設計, 決定是否有需要賦予現實生活處境作為問題的出發點, 又或者以較為抽象的方式提出問題。 數學思考本身需要學生掌握抽象化的方法,也必須學懂處理抽象的問題, 而且抽象的、脫離生活現實的難題也可以有很高的趣味性, 千萬不要因著「處境化學習」的片面、偏頗的提法, 而忽略了運用這方面教學材料的意義和價值, 至少有部分學生是值得利用這種方式、進路來加以啟發的。 順帶一提,在「目標為本課程」的實施中, 一些學校的教師想方設法擬就現實生活情境來貫串作為評估課業及測驗、 考試試卷中所有題目的處境,這種做法恐怕既浪費了教師的時間, 又未必能恰當地對應所有有關的評估目標,其實大可不必。 事實上,傳統的、簡單的、單項的測試題目同樣能夠有效地評核學生的學習成果, 重要的反而是教師必須在擬題前,先釐清預算評核的知識項目和不同層次的認知能力, 再配以恰當的測試題目才是。
最後,僅以一題完全虛假卻不能不如此擬題的文字題作結, 讀者或許會更能揣摩到數學的趣味性與題目情境的關係 (註 [22]):
保羅放下他的書,在一張小紙片上計算著。「這本書裡有很多可讀的東西,」 他告訴他的妻子,「我想你也一定喜歡。」「不要讓我等太長時間!」瓊微笑說,「你還有多少要讀?」
「將近 150 頁,」保羅回答道,「我看這裡有些東西非常奇特。 第一章是從第 13 頁開始的,從這一頁到我現在正看著的前一頁, 那些頁的頁數相加,跟我將要看的那些頁的頁數相加,兩者和是 一樣的。」
「那麼你看的時候有沒有跳過一些頁呢?」瓊問, 「無論如何你等看完書再去算那些東西,我想要書!」
實際上保羅一頁都沒有跳過。試問,他手頭正在讀的是第幾頁?
註釋
| [1] | 可參閱例如 Vershaffel, L., De Corte, E., & Lasure, S. (1994). Realistic considerations in mathematical modeling of school arithmetic word problems. Learning and Instruction, 4, 273-294. Verschaffel, L., & De Corte, E. (1997). Word problems: A vehicle for promoting authentic mathematical understanding and problem solving in the primary school? In T. Nunes, & P. Bryant (Eds.), Learning and teaching mathematics: An international perspective (pp. 69-97). Hove, UK: Psychology Press.及Wong, K.M.P. (1997). Do real-world situations necessarily constitute "authentic" mathematical tasks in the mathematics classroom? Curriculum Forum, 6(2), 1-15. |
| [2] | 先此聲明,本文討論「目標為本課程」時只涉及數學科之教學,其他科目實施 「目標為本課程」的問題完全不在本文範圍。 |
| [3] | Resnick, L. B., & Ford, W. W. (1981). The psychology of mathematics for instruction. Hillsdale, NJ: Lawrence Erlbaum Associates. (見頁14-15。) |
| [4] | 這報導節譯自 Pressey, S. L. (1933). Psychology and the new education. New York: Harper & Brothers Publishers. 第237頁。在書中作者欲以此例子說明測驗題目的有效性受 受試者所處的生活、經濟環境影響頗大,答對問題與否並不全然反映其心智能力。 |
| [5] | 節譯自Baruk, S. (1989). Wie alt ist der Kapitan?: Uber den Irrtum in der Mathematik. Basel: Birkhauser. (How old is the captain?: On the error in mathematics; 法文原著1985年 出版),頁29。相關之引述亦見於Schoenfeld, A.H. (1991). On mathematics as sense-making: An informal attack on the unfortunate divorce of formal and informal mathematics. In J.F. Voss, D.N. Perkins, & J.W. Segal (Eds.), Informal reasoning and education (pp. 311-343). Hillsdale, NJ: Lawrence Erlbaum Associates. |
| [6] | 請參看李秉彝、張奠宙、鄭正亞 (1997)。考試文化與數學教學。《數學教育》, 第四期,頁96-103。 |
| [7] | 據說,有小孩回答船長36歲,提出了這樣一個有趣的理由:船長出生以來,每年他 (她) 的父母親都送他 (她) 一隻羊作為生日禮物。這小孩的想像力何其豐富呢!(惟筆 者找遍手邊的文獻書籍,已尋不著這段小插曲的資料來源。) |
| [8] | 本地在這方面的研究不多,最近我們剛開始這方向的工作,請參看Wong, N.Y., Lam, C.C., & Wong, K.M.P. (1998). Students' and teachers' conception of mathematics learning: A Hong Kong study. Proceedings of ICMI-East Asia Regional Conference on Mathematics Education 1, Volume 2, 375-404. |
| [9] | 題目中的 Bielefeld 和 Frankfurt 均為德國本土人熟悉的大城市。請參看Kilpatrick, J., & Radatz, H. (1983). How teachers might make use of research on problem solving. Zentralblatt fur Didaktik der Mathematik, 15, 151-155. 及 Kilpatrick, J. (1987). Problem formulating: Where do good problems come from? In A.H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 123-147). Hillsdale, NJ: Lawrence Erlbaum Associates. |
| [10] | Saljo, R., & Wyndham, J. (1993). Solving everyday problems in the formal setting: An empirical study of the school as context for thought. In S. Chaiklin, & J. Lave (Eds.), Understanding practice: Perspectives on activity and context (pp. 327-342). Cambridge: Cambridge University Press. |
| [11] | 這裡不妨以維特根斯坦 (Ludwig Wittgenstein) 所談的生活世界 (Lebenswelt) 考慮之。 |
| [12] | 可參閱例如Brown, J.S., Collins, A., & Duguid, P. (1989). Situated cognition and the culture of learning. Educational Researcher, 18(1), 32-42. Lave, J. (1988). Cognition in practice: Mind, mathematics and culture in everyday life. Cambridge: Cambridge University Press. Rogoff, B., & Lave, J. (Eds.). (1984). Everyday cognition: Its development in social context. Cambridge, MA: Harvard University Press. |
| [13] | 可參閱例如 Salomon, G. (Ed.). (1993). Distributed cognitions: Psychological and educational considerations. Cambridge: Cambridge University Press. Winograd, T., & Flores, F. (1986). Understanding computers and cognition: A new foundation for design. Norwood, NJ: Ablex. 這種觀點基本上反對主流認知心理鄭將觀察、活動的主體與被觀察或被霆作的客體 區別、分割開來的思考進路,取而代之是強調人尤如嵌進世界的活動之中受其處境 及活動性質所限制而進行著各種活動。如 Winograd及Flores (1986) 所言︰「我們基本 上通過利用即在手邊的 (the ready-to-hand) 進行實踐活動而接觸世界,在這個世界裡 我們經常不作反思地活動。抽離的反思可以有啟發性,但亦可能同時由於孤立或將 這些現象分類以致搞混了現象本身」(頁32)。他們又舉例說︰「當我拿著鎚子打釘 (而不是想著一個鎚子) 時,根本不必運用鎚子的明確表象 (representation)。我這個 活動能力乃來自我對鎚打的熟悉 (familiarity with hammering) ,而非對鎚子的知識 (knowledge of a hammer)」(頁33)。 |
| [14] | 請參閱 Leont'ev, A.N. (1978). Activity, consciousness, and personality. Englewood Cliffs, NJ: Prentice-Hall. Lektorsky, V.A., & Engestrom, Y. (Eds.). (1990). Activity: Theories, methodology and problems. Orlando: Paul M. Deutsch Press. 又可參閱例如 Nardi, B.A. (Ed.). (1996). Context and consciousness: Activity theory and human-computer interaction. Cambridge, MA: The MIT Press. |
| [15] | 詳細討論請參閱Wong, K.M.P. (1997). Do real-world situations necessarily constitute "authentic" mathematical tasks in the mathematics classroom? Curriculum Forum, 6(2), 1-15. 或黃家鳴 (1997)。生活情境中的數學與學校的數學學習。《基礎教育學報》, 第七卷,第一期,頁161-167。 |
| [16] | 「地穴比諭」可參閱 Plato "The Republic" (Penguin Books, second edition (revised), 1987), Part VII §7 (頁316-325)。在《理想國》(即 "The Republic") 一段蘇格拉底 (Socrates) 與葛樂康(Glaucon) 的對話中,蘇格拉底以此比諭來談論人的天性與追求知識、 真理的關係,人可以如何在認知、理性上提升,又如何達致更高的精神視野。 |
| [17] | 請參閱馮振業 (1997)。《把數學課變得「數學一些」》。論文發表於數學教育研討 會「新時代基礎數學教育」,主辦機構為香港中文大學課程與教學學系,香港, 17.05.1997。 |
| [18] | 可參閱 Wills, H. (1985). Leonardo's dessert: No pi. Reston, VA: National Council of Teachers of Mathematics. |
| [19] | 一些適合小學數學課的簡單遊戲亦足以引介數學概念卻不用什麼「學習情境」作包 裝,請參閱Lopez-Real, F. (1997). Guessing games in primary mathematics. EduMath, 4, 39-46. |
| [20] | 費瑪 (Pierre de Fermat,1601-1665) 曾在他的一本書的頁邊空白處這樣評註: 「不可能將一個立方數寫成兩個立方數之和;或者將一個4次冪寫成兩個4次冪之和; 或者,總的來說,不可能將一個高於2次的冪寫成兩個同樣次冪的和」,而在這個 邊註後面,他還寫下了更惱人的話:「我有一個對這個命題的十分美妙的證明, 這裡空白太小,寫不下。」用代數式來說,即x^n + y^n = z^n方程中當n (冪為整數) 大於 2時,x、y、z並無任何整數解,是為「費瑪最後定理」 (Fermat's last theorem) 。 (當n = 2時,我們熟知x、y、z有整數解,例如3² + 4² = 5² ,5² + 12² = 13²等。) 於是 一代又一代的數學家都曾挑戰這個險峰而無功而回,直至1994年最終由美國數學家 Andrew Wiles 不無波折地完全解決,証明其真確性。有興趣的讀者請看Singh, S. (1997). Fermat's last theorem: The story of a riddle that confounded the world's greatest minds for 358 years. London: Fourth Estate. (中譯本:賽門.辛 (薛密譯) (1998)。《費瑪最後 定理》。臺北:臺灣商務印書館。) |
| [21] | 1742年身為沙皇彼得二世的家庭教師的 Christian Goldbach 寫信給瑞士大數學家 Leonhard Euler,求問於他能否證明每個大於2的偶數必然可以分解成兩個質數 (又稱 素數) 之和,因為他曾仔細考察過幾十個偶數都是如此。例如:4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, …, 20 = 7 + 13, …等。這個命題被稱為「哥德巴赫猜想」 (Goldbach conjecture),至今仍未能被證明,亦未被證偽。 |
| [22] | 節錄自Hunter, J.A.H., & Madachy, J.S. (1975). Mathematical diversions. New York: Dover Publications, Inc. (p.119) (中譯本《數學娛樂問題》(張遠南、張昶譯),上海教育出版 社 (1998),頁133。) 本題答案:全書有483頁,而保羅正在讀第342頁。本題其中之 一個條件為「還有將近150頁書未讀」,即未讀的頁數少於150,而前述答案中未讀 的頁數實為141頁。若題目改為「還有大約150頁左右的書未讀」的話,則答案還可 以多一個可能性,即全書有542頁,而保羅正在讀第384頁,而未讀的頁數則為158 頁。 |