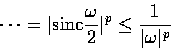1 (是
![]() Page 96
Line -10
Page 96
Line -10
1 (是
![]() )
)
![]()
![]() Page 97 Line 10
Page 97 Line 10
![]() Page 105 Line 5
Page 105 Line 5
![]() Page 105 Line -6
Page 105 Line -6
![]() Page 120
Line -7
Page 120
Line -7
則
(un)*(vn) 必定存在,而且
(un)*(vn)=(vn)*(un)。
![]() Page 124
Line -7 - -5
Page 124
Line -7 - -5
![]() 。兩個泰勒級數的極限函數 (如果存在),若在一段區間 [a,b] 內相等,
則兩函數必定相等;兩個傅立葉級數的極限函數 (如果存在),
可能在一段區間 [a,b] 內相等,但在區間之外不相等。
。兩個泰勒級數的極限函數 (如果存在),若在一段區間 [a,b] 內相等,
則兩函數必定相等;兩個傅立葉級數的極限函數 (如果存在),
可能在一段區間 [a,b] 內相等,但在區間之外不相等。
![]() Page 129
Line 5
Page 129
Line 5
![]() 刊在英國 Nature 雜誌上的文章。
刊在英國 Nature 雜誌上的文章。
![]() Page 138 Line 12
Page 138 Line 12
![]() Page 139 Line 7
Page 139 Line 7
![]() Page 144 Line 11
Page 144 Line 11
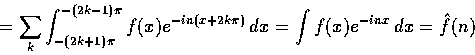
![]() Page 152 Line -4
Page 152 Line -4