![]() Page 173 Line 2
Page 173 Line 2
![]() Page 173
Line -4
Page 173
Line -4
所以
![]() ;
;![]()
![]() Page 186 Line 3
Page 186 Line 3
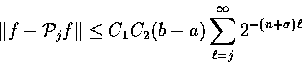
![]() Page 204
Line 5
Page 204
Line 5
![]() 因為每單位長內有
2j + (2p-2) 個
因為每單位長內有
2j + (2p-2) 個
![]() ,
,![]()
![]() Page 206
Line 9 - 10
Page 206
Line 9 - 10
故
![]() 在
在 ![]() 附近的圖形是平坦的。
當 j 越大時,
附近的圖形是平坦的。
當 j 越大時,
![]() 在
在 ![]() 附近就有越大的範圍圖形是平坦的 (因為圖形膨脹了)。
附近就有越大的範圍圖形是平坦的 (因為圖形膨脹了)。![]()
![]() Page 207
Line -10
Page 207
Line -10
![]() 當
當 ![]() 靠近 0
靠近 0
![]() Page 208
Line 1 - 2
Page 208
Line 1 - 2
![]() 高頻部分 (high frequency part)。
高頻部分 (high frequency part)。
![]() 高頻濾波係數 (high-pass filter coefficients)。
高頻濾波係數 (high-pass filter coefficients)。
![]() Page 211
Line 5
Page 211
Line 5
頻率域的函蓋是
![]() ,但是
,但是 ![]()