
其實我早就知道 — 而且經常說 — 大多國中生沒有習得指數律。而且,我認為根本原因是國中階段沒有利用指數做計算的合理動機,當然也沒有需求。但是我這次還是上當了。原因(不是推諉)實在是因為太相信心測中心。因為我知道心測中心安排的第一題是有預試實驗基礎的「基礎」題,它應該是絕對有把握的簡單題目,要保證 — 我們總是開玩笑說 — 教育部長也會做。所以,雖然我心底懷疑此題沒那麼簡單,還是猜測此題的答對率可達 85%。沒想到實際上只有 75%。
國中階段僅在七年級上學期出現過合理的指數記號需求:正整數的標準分解式。但是,此處僅有紀錄的需求而沒有計算的需求。而且,即使是此需求,也在隨後三年的數學課程中不再出現,學生沒有「學而時習之」的機會,於是指數律,乃至於指數記號,在國中階段就是孤立的的存在,必須刻意地學習,於是很容易成為惰性的(只能硬背)知識。
考生在此第一題的實徵表現,再次鞏固了我的概念:國中階段的指數課程,
- 如果有上位理由認為它必要,就該認真思考它在國中階段的實用性與合理性,讓學生有機會真正習得;
- 如果沒有上位理由支持它必要(我認為沒有),則應乾脆從國中課程抽離,徹底留到高中。
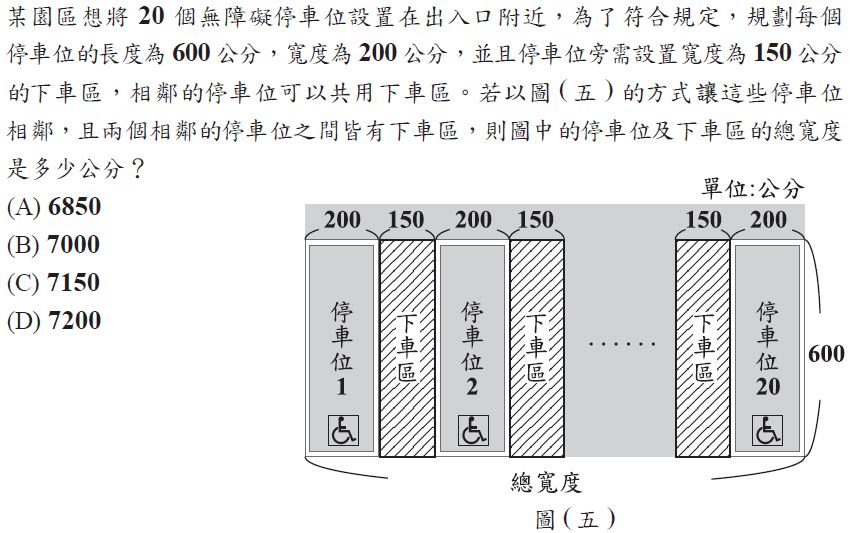
我猜想命題/組卷者的意圖是將此題視作「有規則的數列/級數」。但是我認為這題不就是小學階段的一種標準題型嗎:植樹問題 — 或稱電線桿問題 — 而且此題是最基本型的植樹,毫無變化。我估計答對率 80%,實際是 71%。
於是我擔心:是不是國小已經取消植樹問題了?或者,是不是越來越多小學教師不會教植樹問題了?

雖然我認為此題「無聊」,但是畢竟太直白、太簡單,於是我估計答對率 80%,實際卻是 60%。這樣的結果真是給了我一顆震撼彈;以前我確實沒有關心過這個內容,即使我認為「解的個數」並無刻意學習的必要:若能從經驗中歸納出來最好,若沒有察覺也無所謂,重要的是能夠求解,並且能夠將數學解「擬合」(fit-in) 到情境之內;這件事可以分成以下幾項:
- 判斷所得的解「合不合」情境;這一點全國教師都做得很好。
- 取得適合情境的「可行解」,通常就是取概數的意思。這一點,只有使用計算機才能做。
- 詮釋解的意義,藉以改進數學模型或提出其他解決方案。例如當情境只允許某些正整數,則數學解未必合適,反而應該換成另一個數。
但是我一直以為,即使這是一個沒必要的內容,放在課程裡也無所謂,因為我以為它很簡單,多學這件內容並沒有增加認知負荷。但是這一題的實徵經驗,讓我驚覺:「解的個數」可能不是所謂「即使無益但也無害」的學習內容,它可能是「有害」的內容。就像指數律,要商量將它移除。
會議中,有老師懷疑是不是「虛根」影響了學生,導致答對率下降?我不相信「虛根」造成任何影響,這位老師想太多了。而且,細看三類成就的學生在四個選項的分布,很明顯高分組考生的答題狀況正常,是中、低分組的考生拉低了整體答對率,我更不能相信中、低分組考生受到「虛根」觀念的干擾。

雖然我認為此題簡單,但是我知道:只要教授認為一題「漂亮」,這題就「難」;而我認為此題漂亮。所以我刻意調低此題的答對率為 50%,沒想到實際更低:43%。
面對這樣的表現,我做個事後諸葛的預測:因為考生缺乏動態操作函數圖形的經驗。再仔細反省一下,此題讓我感覺「漂亮」的原因是它的動態想像;我猜想命題老師一定有函數圖形動態變化的視覺經驗,而且很可能不是被動地觀賞,而是主動操作軟體控制它的變化。可是大多數考生沒有這種經驗,無法想像圖形的移動變化,可能根本不懂題目在問什麼?
我想要堅持這個題目的評量目標是正當的,是有必要的,所以不該在未來的課綱中移除,也不該在未來的考試中避免。反而應該讓此題型廣為周知,促使更多國中教師提供動態圖形變化的學習經驗。108 課綱已經刪除了九年級的「二次函數配方」,國中學生節省了代數操作的精力,有更多時間專注於建立圖形的經驗,希望國中教師多幫忙,把二次函數的教學時間與要點,從代數轉移到圖形。