數學課程綱要
分數 vs 小數的數學史啟示
洪萬生老師出版的一套四冊《數之軌跡》賜給我開授「數學史」選修課的契機;如果沒有這套書,我就找不到適合支持一學期大學部選修課程的數學史教材。但我的授課計畫宣告這門課是為了支持數學教育,所以我用「數學史應用於數學教育」的濾鏡將這套書的內容傳遞給學生。如我預期的,閱讀經驗經常觸發教育方面的想像。這篇散文分享第 I 冊第 2
章的啟示。
- 洪萬生編(2024)。數之軌跡 I—古代的數學文明。三民。
這一章開頭就寫 (p.24):
蘇美和埃及是世界上有紀錄的最早的文明。而他們之所以有紀錄,就是因為他們發明了文字:蘇美文和埃及文 — 而不是中文 —
是世界上最早的文字。我呼應這段話,提醒讀者:
有文即有數
數字至少是跟文字同時被發明的。甚至,站在數學老師的立場,我更猜測:文字是伴隨數字而發明的。先人可能是先因為記下數量的需求而發明數字,同時為了分辨數量的所指而創造了最初的文字。但數字並不是古早的計算工具。各地的古文明不約而同發明數字 —
在那之前早就有口語的數詞 —
但從來不是為了計算(筆算),而是為了記錄。各民族都另外發明了計算的工具,如今通稱為算盤。所以自古以來計算都用工具,數字只用來記錄計算的結果。直到紙筆(也許還有橡皮擦)變得足夠普遍之後,搭配印度─阿拉伯數碼的筆算才流行起來,而華人社會普遍採用筆算的歷史,可能不到 150
年—可能是從第二十世紀才開始的。因為:
歷來計算皆用工具
工具的材料從土石變成竹簽變成木丸變成金屬齒輪,最後變成電流,它們一脈相承全都是計算的工具。由此可見,我們今天直到高中階段的數學教育都還強調筆算,不准許學生使用工具,實在是嚴重違逆了歷史的潮流。
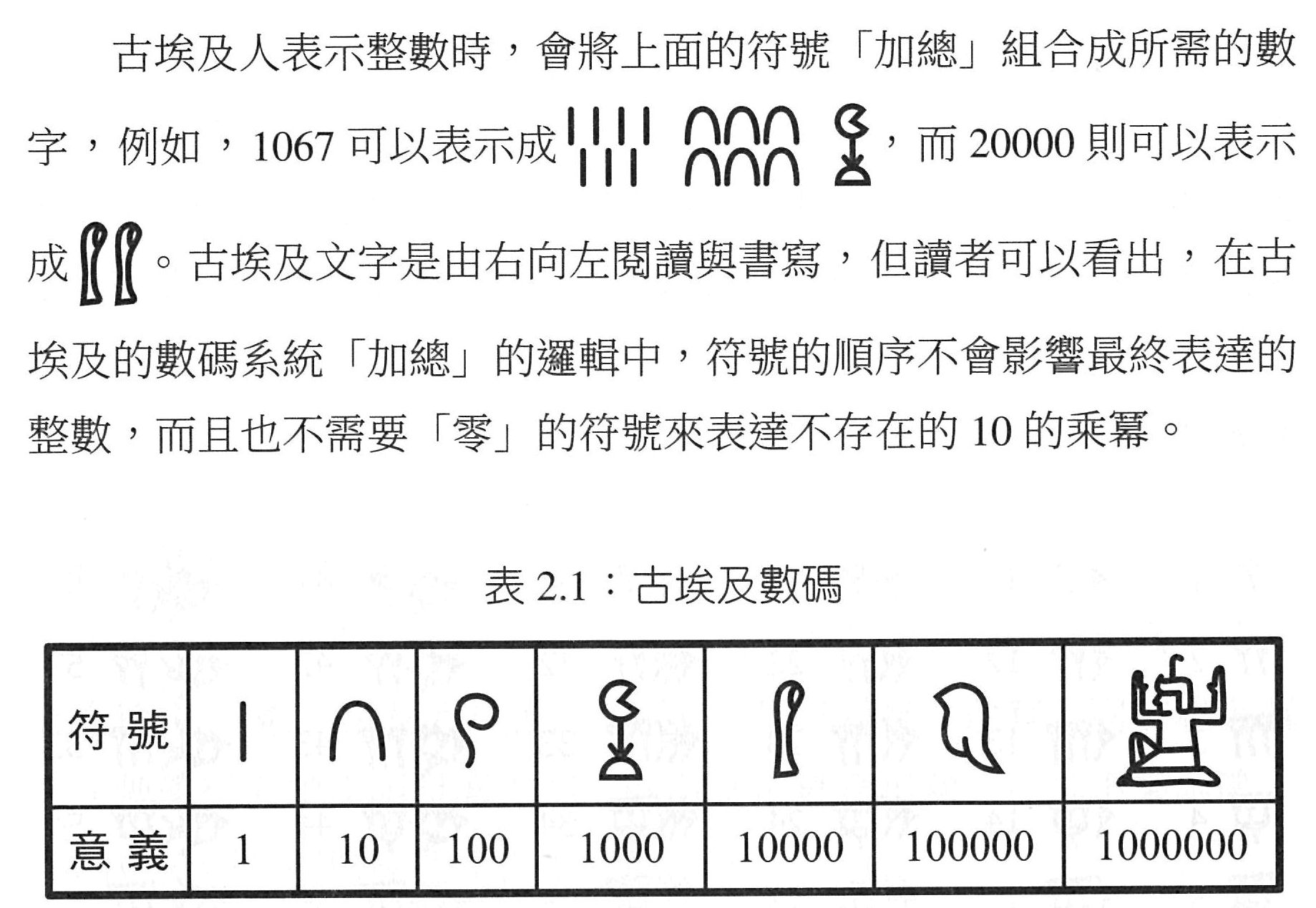
接下來,書裡介紹了埃及人的數碼與數字,重點是
- 埃及有十進制的數碼
- 但是埃及沒想到對位的計數系統
所以埃及數字不一定要從高位寫到低位,卻需要把代表 10 的次方的數碼(個十百千萬等)全都加起來,如以下第 25 頁內容。
想必在他們的語言中,有一二三四等數詞,可是數字系統並沒有寫出來。這是因為:雖然埃及文書用「拾拾拾拾拾拾」記錄六十,我實在不能相信他們說話的時候,會說「拾拾拾拾拾拾」來表達六十!
相對的,蘇美數字使用六十進制的數碼,而且發明了位值概念。蘇美人可以重複使用六十進制的 59 個數碼 —
他們也許沒有固定的佔位符號(也就是「零」),但是在實用中肯定有佔位或提醒讀者「缺位」的書寫方法 — 如下圖(第 26 頁)。
用六十進制數字 \((1,0)_S\) 表示數值時,它相當於 60;其中足標 S
是 Sexagesimal 的縮寫。依此類推,則
\[(11,22,33)_S=11\times60^2+22\times60+33=3,9600+1320+33=4,0953\]
但這一章最精彩的是埃及、蘇美處理「零頭」(fraction)
的方式。不論使用怎樣的單位,只要測量連續量就難免有零頭。埃及文用分數處理零頭,蘇美文用小數。理論上我們知道小數是分數的特例,從這個數學觀點來看,似乎人們應該先了解分數,才能了解小數。但是從埃及、蘇美兩個古文明的經驗來看,也許未必如此。從《數之軌跡》內容來看:埃及人只用分數,蘇美人只用小數。而不論「只用分數」或者「只用小數」似乎都可以發展出頗為複雜的文明。這個現象帶給數學教育的啟示之一是:
小數未必須從分數推導出來
反過來看,如果先學習小數 — 這樣更貼近當今社會中的生活經驗 —
則小數可以作為分數的前置經驗。
蘇美文沿用整數的 59 個數碼,可以表達任意多位的小數零頭。例如我們用
\((0; 44, 55, 6)_S\) 表示六十進制的三位小數,其中小數的位名依序採用分、秒、忽,則它讀作 44 分 55 秒 6 忽,另記作
\(44^\prime\;55^{\prime\prime}\;6^{\prime\prime\prime}\);它的數值意義是
\[44^\prime\;55^{\prime\prime}\;6^{\prime\prime\prime}
=\frac{44}{60}+\frac{55}{60^2}+\frac{6}{60^3}
=0.748638888\cdots\]
蘇美人很可能也有分數觀念,只是不用它而已。理由是:他們選擇六十進制,很可能是因為六十有很多因數,因此許多常用的分數零頭 —
例如二分之一、三分之一、四分之一、五分之一、六分之一,乃至於十二分之一、十五分之一、二十分之一等 —
在六十進制的小數中,都是一位小數。例如
\(\displaystyle\frac12=30^\prime\)、\(\displaystyle\frac1{4}=15^\prime\)。這個好處,或許就是人們一直習慣採用六十進制計時,而不願意把時間改成十進制的原因。
分、小數各有互補的優缺點
分數和小數各有優缺點,而且它們頗為互補:
- 分數
- 優點:當真解為有理數時,沒有誤差。
- 缺點:實踐分數結果時,通常有測量或支付的困難。
- 小數
- 優點:較容易搭配測量工具、貨幣實踐小數結果。
- 缺點:即使真解是有理數,通常仍有誤差。
或許就是因為這樣的互補性,使得這兩種表達零頭的方式,各有擅場而不能定於一尊,於是源自古代埃及、蘇美的這兩種表達零頭的數,都一直流傳到今天。關於分、小數優缺點的比較,也可參閱另一篇短文〈分、小數本事〉。
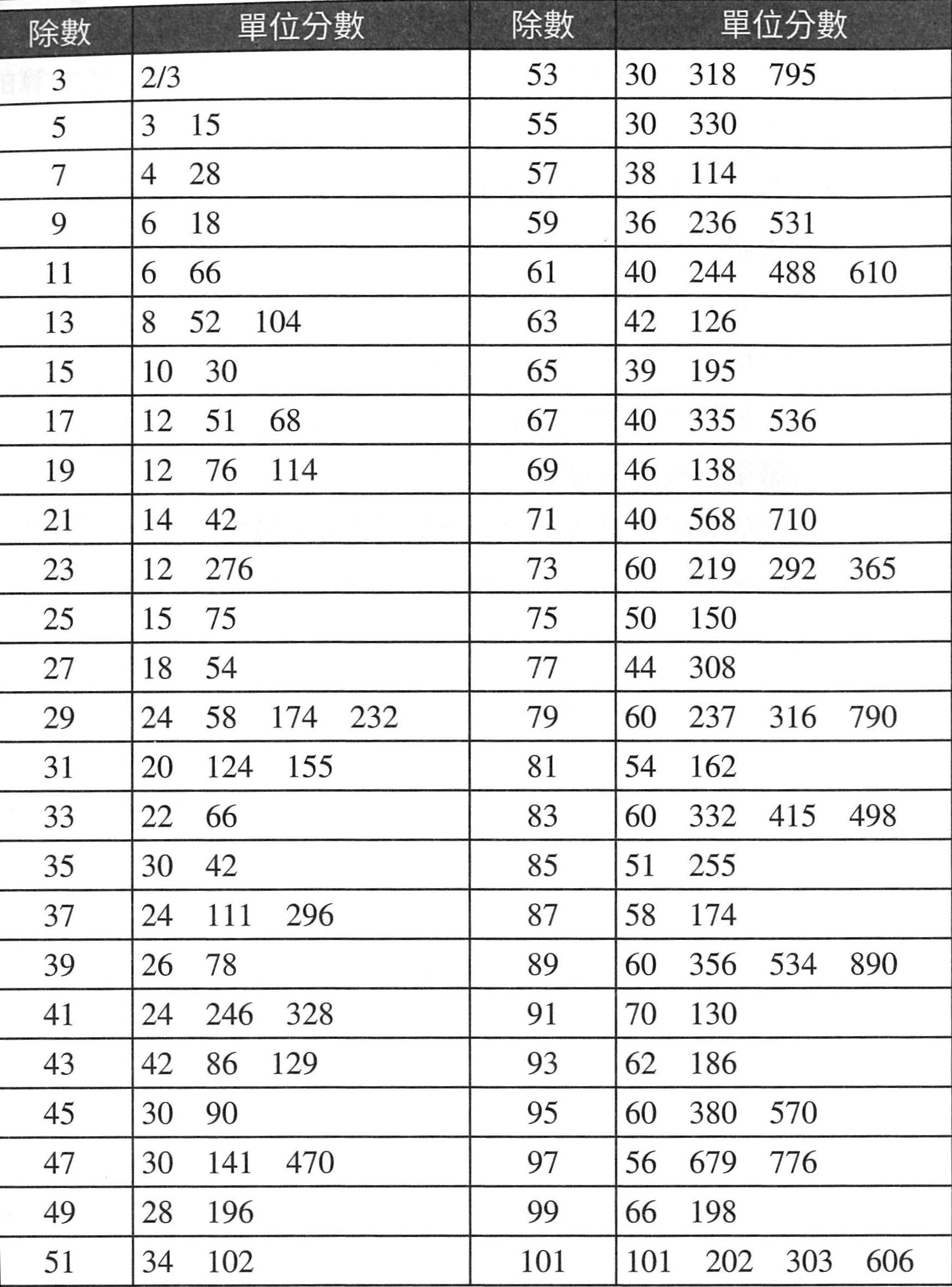
埃及人很可能早就體驗了分數「難以實踐」的缺點(或挑戰),發明了「單位分數」分解法。除了分母為 2 或 3 的分數以外,古埃及算家與工匠將分子大於 1 的分數換成單位分數之和,如下文所載(第 29 頁)。
書中第 32 頁附上分子為 2 時,101 以內各分母(當然取奇數即可)的單位分數之分解:
舉例說明表格的用法:例如左欄的 5 和 7 表示
\[\frac25=\frac13+\frac1{15},\quad\frac27=\frac14+\frac1{28}\]
可觀察分解之後的第一個單位分數的分母比較小。
至於 \(\displaystyle\frac23\)
不拆成單位分數之和;雖然它仍可以分解,但是埃及人不這樣做:
\[\frac23=\frac12+\frac16\]
沒有史料真的能解釋埃及人為什麼要將分數拆解為單位分數?這樣做,對於異分母分數的加減運算並沒有明顯的好處。我認為埃及不拆解 \(\displaystyle\frac23\)
這件事提供了一條線索,那就是
埃及拆解分數為實踐
所謂「實踐」意思是真的從整體分割出來,例如分割一塊地、一筆稅金、一段時間,或者製造一個斜坡(斜率為指定的分數)。因此,不拆解 \(\displaystyle\frac23\)
的原因很明顯:它已經很容易實踐。至於其他「分之二」,則在拆解之後同時獲得了概數與誤差。例如
\[\frac27=\frac14+\frac1{28}\]
表示 \(\displaystyle\frac27\) 大約等於 \(\displaystyle\frac14\),
而誤差是 \(\displaystyle\frac1{28}\)。
分數 \(\displaystyle\frac14\) 顯然比 \(\displaystyle\frac27\)
容易實踐。當實際環境可以實踐
\(\displaystyle\frac27\),那就實踐即可;當它不容易實踐,則可以換成較容易實踐的
\(\displaystyle\frac14\),而埃及人知道此時的誤差是 \(\displaystyle\frac1{28}\)。我猜他們不會補足那 \(\displaystyle\frac1{28}\),因為:如果可以實踐
\(\displaystyle\frac1{28}\),那麼當初不就直接實踐 \(\displaystyle\frac27\)
即可?假如他們認為可以接受 \(\displaystyle\frac1{28}\)
這樣的誤差,那就好;如果不能接受,他們可能再取容易實踐的近似值,例如
\[\frac1{28}\approx\frac1{32}\quad\text{或}\quad
\frac1{28}\approx\frac1{24}=\frac18\times\frac13\]
等等。而 \(\displaystyle\frac1{32}\)
之所以較容易實踐,是因為它只要連續折半:做五次折半。實際的操作,受限於當時的測量工具以及工匠的手藝,我們就不再深入考究了。
那麼為什麼只有「分之二」的表格呢?或許考古學家沒發現其他表格,但我猜想埃及人是真的不製造其他分數表格,因為「分之三」就是「分之二」加上「分之一」,而「分之四」就是兩倍的「分之二」,依此類推。