數學英文

多邊形外接圓

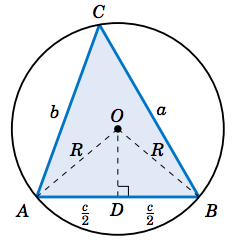
通過多邊形所有頂點的圓，稱為那個多邊形的外接圓 (circumscribed circle / circumcircle)： The circle that passes through all the vertices of a polygon。 並非所有多邊形都有外接圓， 但是因為不共線三點決定一個圓，所以三角形一定有外接圓。 （凸）四邊形必須滿足「對角互補」的條件才有外接圓（opposite angles are supplementary）， 這種四邊形的頂點稱為共圓 (concyclic)。 正多邊形的頂點必然共圓：Vertices of a regular polygon are concyclic points， 這些頂點將外接圓分割成相等的圓弧 (cut the circle into congruent circular arcs)。

當多邊形有外接圓時，它的圓心稱為多邊形的「外心」(circumcenter)， 它的半徑為「外半徑」(circumradius)。 它是多邊形任兩邊的中垂線交點：

the intersection of the perpendicular bisectors of any two sides of the polygon

三角形邊角關係 (the side-angle relationships) 的定性描述 (qualitative descriptions) 為

• 大邊對大角，小邊對小角
  In any triangle, the greater side subtends the greater angle.
• 大角對大邊，小角對小邊
  In any triangle, the greater angle is subtended by the greater side.

正弦定理 (Law of Sines) 即為三角形邊角關係的定量描述 (quantitative descriptions)： 邊長與其對角之正弦的比值為常數，此常數為三角形外接圓的直徑， 或者說是兩倍的外半徑。

The ratio of a side of a triangle to the sine of its opposite angle is a constant. The constant is the diameter of the triangle's circumcircle, or \(2R\) where \(R\) is the circumradius.