數學英文
分小數互換
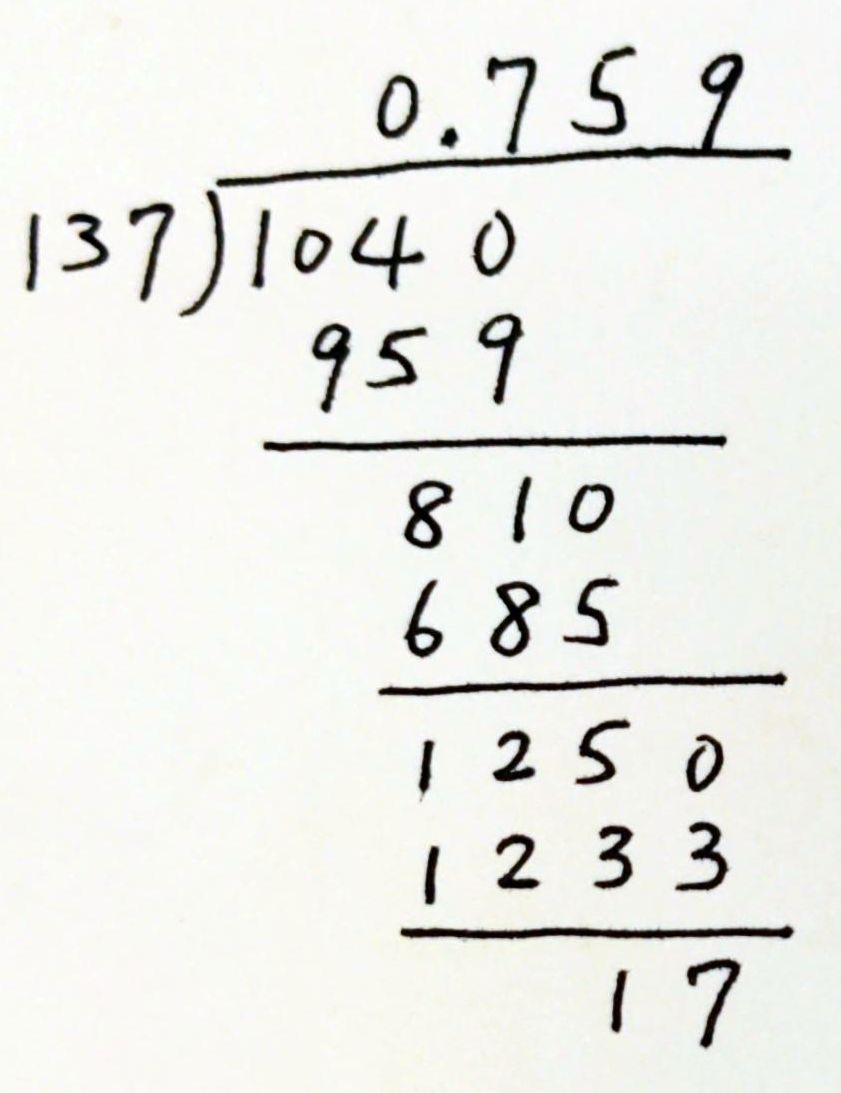 分數和小數是同一種數──不足一的數──的兩種表達方式。
以前不常用小數,是因為只有分數才能算出正確結果,小數經常不精確。
但是後來發現分數雖然精確但是難以實踐,小數雖然有誤差但是可以解決實際問題。
例如將近 2000 年前的《九章》有一題答案是
\(\displaystyle8{104\over137}\) 元這種金額:它雖然正確但是難以支付。
幸好後來有了轉換分數為小數 (convert fractions to decimals) 的演算法 (algorithm),就是我們在小學學過的直式除法/長除法 (long division),如右圖,
其中
分數和小數是同一種數──不足一的數──的兩種表達方式。
以前不常用小數,是因為只有分數才能算出正確結果,小數經常不精確。
但是後來發現分數雖然精確但是難以實踐,小數雖然有誤差但是可以解決實際問題。
例如將近 2000 年前的《九章》有一題答案是
\(\displaystyle8{104\over137}\) 元這種金額:它雖然正確但是難以支付。
幸好後來有了轉換分數為小數 (convert fractions to decimals) 的演算法 (algorithm),就是我們在小學學過的直式除法/長除法 (long division),如右圖,
其中
 稱為除法括號 (division bracket 或 long division symbol)。
稱為除法括號 (division bracket 或 long division symbol)。
分數與小數這兩種表達形式 (expressions) 的轉換,
寫成等式 \(\displaystyle8{104\over137}=8.759\cdots\),其中 \(\cdots\) (點點點,dot-dot-dot)是省略號 (ellipsis),
讀作 et cetera 或 and so forth。
這個等式可以說成 \(\displaystyle8{104\over137}\) 的小數表達
(expressed in decimal form) 是 \(8.759\cdots\)。
配合社會上出現「角/毛」(dime: 1/10 of a dollar)、「分/毫」(cent: 1/10 of a dime) 這些貨幣,
雙方可協議將 \(\displaystyle8{104\over137}\) 這種金額,
改為支付 8 元 7 毛 5 分或 8 元 7 毛 6 分 (8 dollars 76 cents);
雖然不精確,但是可執行。
所有分數都可以轉換成小數,當化為最簡分數之後的分母僅有 2 和 5 兩種質因數時:
there are only prime factors of 2 and 5 in the denominator
那樣的分數可以轉換成有限小數,其他分數都轉換成循環小數。
反過來,有限小數和循環小數都可以轉換成分數,
但是不循環的無窮小數都不能轉換成分數。
例如
\[0.10010000100\cdots\]
在小數點下第 1、4、32、42、... 位為 1 其他位皆為
0 的無窮小數,不能轉換成分數。
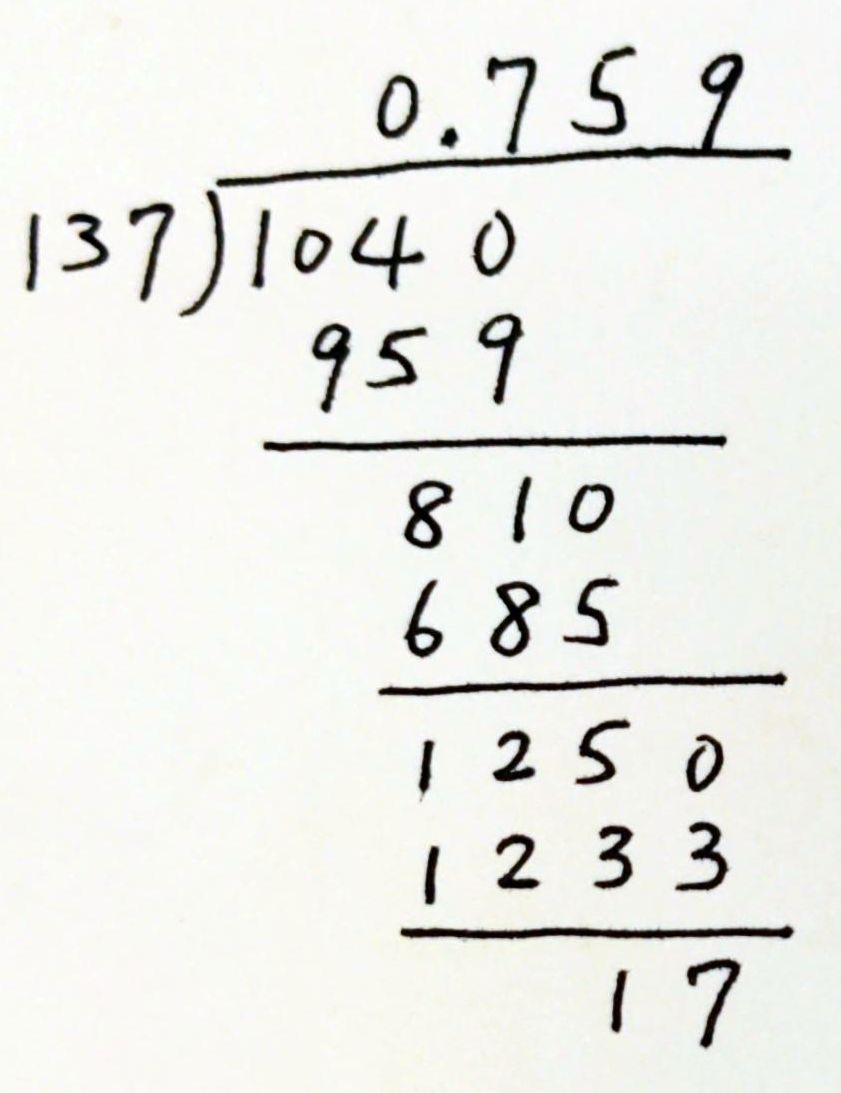 分數和小數是同一種數──不足一的數──的兩種表達方式。
以前不常用小數,是因為只有分數才能算出正確結果,小數經常不精確。
但是後來發現分數雖然精確但是難以實踐,小數雖然有誤差但是可以解決實際問題。
例如將近 2000 年前的《九章》有一題答案是
\(\displaystyle8{104\over137}\) 元這種金額:它雖然正確但是難以支付。
幸好後來有了轉換分數為小數 (convert fractions to decimals) 的演算法 (algorithm),就是我們在小學學過的直式除法/長除法 (long division),如右圖,
其中
分數和小數是同一種數──不足一的數──的兩種表達方式。
以前不常用小數,是因為只有分數才能算出正確結果,小數經常不精確。
但是後來發現分數雖然精確但是難以實踐,小數雖然有誤差但是可以解決實際問題。
例如將近 2000 年前的《九章》有一題答案是
\(\displaystyle8{104\over137}\) 元這種金額:它雖然正確但是難以支付。
幸好後來有了轉換分數為小數 (convert fractions to decimals) 的演算法 (algorithm),就是我們在小學學過的直式除法/長除法 (long division),如右圖,
其中
 稱為除法括號 (division bracket 或 long division symbol)。
稱為除法括號 (division bracket 或 long division symbol)。