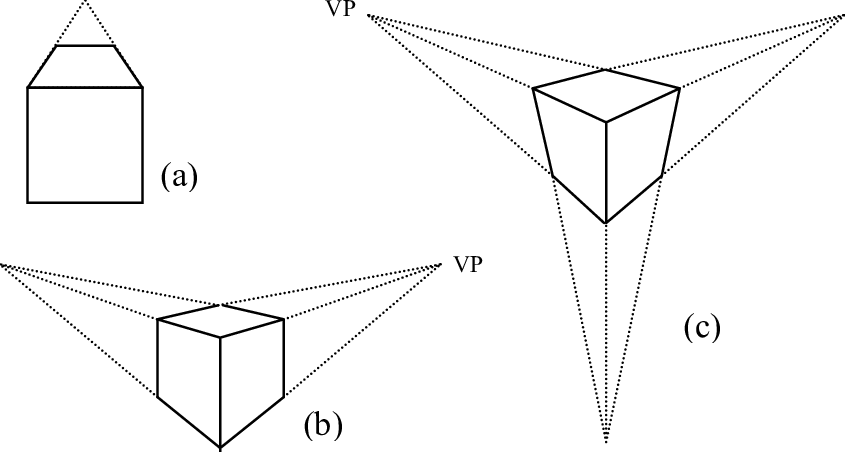
有 (a) 一個、(b) 兩個、(c) 三個消失點的立方體透視圖。
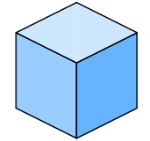
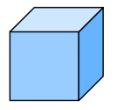
立方體的正視圖(左)與斜的平行視圖(右)。
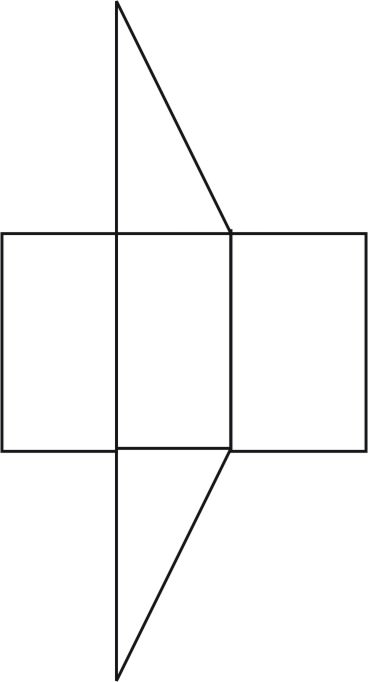
三角柱 (prism) 的一種展開圖。



立方體的正視圖(左)與斜的平行視圖(右)。

三角柱 (prism) 的一種展開圖。
在平面上表現立體物 (representing solids on a plane) 是數學溝通 (mathematics communication) 的重要項目, 它是畫法幾何 (descriptive geometry) 在學校課程中的簡單應用。 數學課專注於視圖的基本原理,在工程 (engineering)、設計 (design)、電腦圖學 (computer graphics) 等領域有更專業的發展,通稱為三維投影 (3D projection)。
首先要了解:數學不採用透視圖 (perspective projection), 所以數學的立體物圖示跟視覺經驗、攝影 (photography)、美術繪圖 (drawing) 有所不同。 在透視圖裡,物體上互相平行的稜邊可能朝向消失點 (vanishing points) 而靠近, 所以它們在平面圖上並不平行。 下圖呈現有一個、兩個、三個消失點的立方體透視圖;我們看到有些正方形變成梯形。
相對地,數學圖示採用平行視圖/平行投影 (parallel projection), 意思是固定一個成像的平面 (image plane) 或投影面 (projection plane), 以彼此平行的視線 (lines of sight 或 sight lines 或 visual axes) 或投影線 (projection lines) 將物體投影在平面上。 因為真正的視線應該交於觀察點 (viewpoint) 而非平行, 所以平行視圖並不符合視覺經驗, 可是它確保空間中彼此平行的直線,在圖示中也是平行的, 所以它適合數學溝通之用。
當平行視圖的視線垂直於投影面時,稱為正視圖/正投影/正射影 (orthographic projection)。 當正視圖同時呈現立方體的三個面時,它們都是非正方形的菱形,如以下的左圖; 而斜的平行視圖 (oblique projection) 反而可以看到一個正方形,如以下的右圖。 正視圖和斜視圖都是常用的圖示法。
三視圖 (three-view drawing 或 multiview projection) 是特殊的正視圖。 想像我們按一般的習慣建立空間坐標:\(x\) 朝向自己,\(y\) 軸朝右,\(z\) 軸朝上。 想像物體放在第一卦限,盡力讓它有最多的面平行於坐標平面, 有最多的稜(或對稱軸)平行於坐標軸。 這時候,物體在 \(yz\) 平面的正射影稱為前視圖 (front view), 也常稱為立面圖 (elevation view); 在 \(xy\) 平面的正射影稱為上視圖/俯視圖 (top view), 也常稱為平面圖 (plan view); 物體在 \(xz\) 平面的正射影稱為側視圖或右視圖 (lateral/side view)。 有必要的話,三視圖最多可以給六幅圖,這六幅圖都稱為主視圖 (primary views); 沒必要的話,也可以只給其中一幅主視圖,例如呈現一片很薄的板子,就只需要上視圖。 有些設計軟體會把視窗分割成四塊,其中三塊呈現三幅主視圖, 第四塊呈現一幅輔助圖 (an auxiliary view), 它是某種視角 (viewing angle) 的正視圖。
生活中的長方體物件,例如書桌、衣櫃、樓房,前視圖的長方形兩邊會說寬 (width) 和高 (height),而上視圖的長方形兩邊則會說寬和深 (depth)。 如果長方體有一邊很短,則會稱那一邊為厚 (thickness)。
另外兩種有助於了解立體物的平面圖是展開圖 (net) 和截面圖/剖面圖 (cross-sections)。例如右圖是三角柱的一種展開圖 (a net for the prism)。 展開圖有助於計算立體物的表面積 (surface area), 而剖面圖有助於用積分計算立體物的體積。
| [語音講解:solids.mp3] |