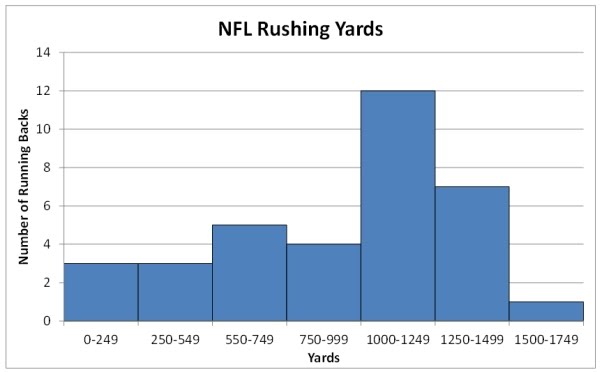
長條圖 (bar chart) 也可以用來呈現連續型資料 (continuous data)。 連續型資料的值就是某個範圍/區間內的實數, 只能針對分組資料 (grouped data) 統計各組的次數分布 (grouped frequency distribution)。 連續型資料的次數分布長條圖, 縱軸是次數或相對次數, 橫軸是分組資料的各組區間,各長條的左右邊界就畫在組界上, 所以長條與長條之間沒有間隔 (has no gaps),如下圖。

數學教材經常把「無間隔的長條圖」(a bar chart without gaps between bars) 稱為「直方圖」(histogram),一般人也的確常這樣說。 或者,有人乾脆規定長條圖僅處理離散型資料,這樣倒也乾脆。 但是,畢竟直方圖原本的專業定義就是讓縱軸表示次數密度 (frequency density), 意思是以各長條(長方形)的面積作為次數──前面說的次數都可以改為相對次數, 這樣導致直方圖有兩種款式:一種以高度為次數,另一種以面積為次數。 以面積為次數的直方圖,可以作為黎曼和的前置經驗, 以面積為相對次數的直方圖,可以作為機率密度函數的前置經驗, 這兩項特色,都支持數學課程應該採用「面積作為次數」當作直方圖的定義, 而將「高度作為次數」視為無間隔的長條圖。
以面積表示次數的直方圖,可容許不等的組距,就像黎曼和可容許不均勻的分割。 下圖是個非等組距直方圖 (histogram with unequal class widths), 同時畫出次數折線圖: 英文是 frequency polygon,所以也譯作次數多邊形。
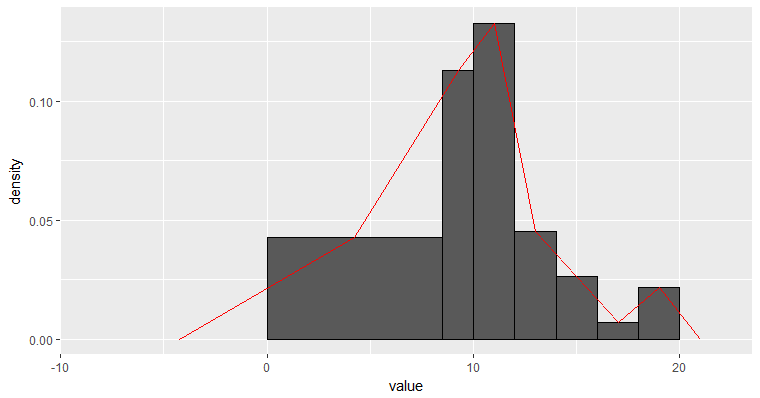
對於離散型資料,或分組的連續型資料,都可以畫次數折線圖 (line graph)。 折線圖是呈現「分布」的另一個好辦法。
連續型資料的累積次數圖 (cumulative frequency diagram) 是一條連續而不遞減的曲線, 稱為累積次數曲線 (cumulative frequency curve)。 離散的有序資料則用折線圖表現累積次數,英文是 cumulative frequency polygon, 所以也譯作累積次數多邊形。 在累積次數圖上,可以精確定義四分位數 (quartiles) 和百分位數 (percentiles), 但是對於離散型資料而言,先作折線圖再計算各分位數不見得方便, 所以產生了許多種不同的計算各分位數規則, 它們全都符合「分位數」的意義,而且它們算出來的「中位數」都一致。
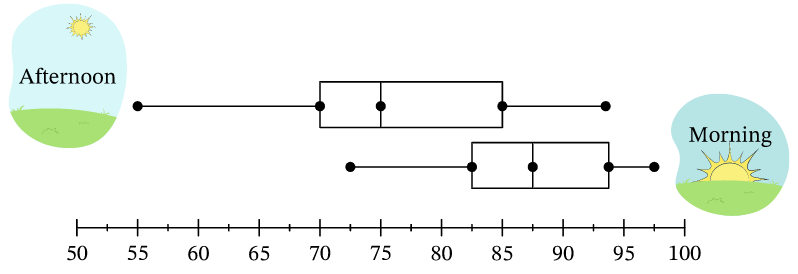
所謂五數概括法 (five-number summary) 是用最小值、三個四分位數、最大值這五個數, 概括描述一組數據的分布情形。將這五個數圖像化的統計圖就是盒狀圖 (box plot), 又稱為盒鬚圖 (box-and-whisker diagram)。 在同一個參考坐標上並列不同組資料的盒狀圖,特別有助於做比較,如下圖。
| [語音講解:histogram.mp3] |