只有當函數 \(f:X\to Y\) 在定義域 (domain) \(X\) 與對應域 (codomain) \(Y\) 之間是「一對一且映成」(one-to-one and onto) 的時候,\(f\) 才有反函數 (inverse function),記作 \(f^{-1}\),讀作 f inverse; 反函數的關係是互相的,也就是說
The inverse of \(f^{-1}\) is \(f\).記作 \[\left[f^{-1}\right]^{-1} = f\] 有反函數的這種函數稱為 bijective(形容詞),其名詞為 bijection;例如說
The inverse of \(f\) exists if and only if \(f\) is bijective / \(f\) is a bijection.Bijection 的中譯為對射或雙射,並不常講,不妨直接說英文。
所謂函數 \(f\) 的圖形 (the graph of a function \(f\)) 就是方程式 \(y=f(x)\) 的圖形。 函數圖形與方程式圖形的差別,在於根據函數的定義,函數圖形必須通過鉛直線檢驗 (vertical line test):曲線與鉛直線至多只有一個交點:
The vertical lines intersect the curve in at most one point.而 bijection 的函數圖形必須同時通過鉛直線檢驗與水平線檢驗 (horizontal line test):曲線與水平直線至多只有一個交點。
函數 \(f\) 的自然定義域 (natural domain) 意思是使得 \(f(x)\) 可以算出一個值的所有實數 \(x\): \[\{x\in\mathbb{R}\mid f(x)\text{ exists}\}\] 當函數在它的自然定義域裡不是 bijection, 可能可以縮小定義域的範圍,在這個比較小的定義域裡,函數是 bijection 而它就有反函數。
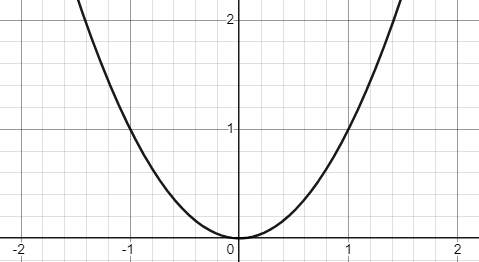
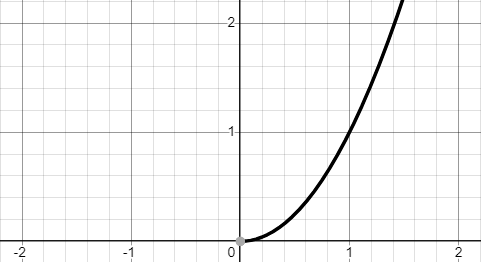
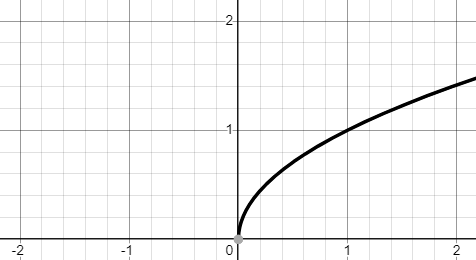
例如 \(x\mapsto x^2\) 的自然定義域是 \(\mathbb{R}\), 以下左圖是它的函數圖形,顯然不能通過水平線檢驗。 但如果將定義域設定在 \(x\in[0,\infty)\),如中圖,就通過了; 所以 \(x\mapsto x^2\) 在 \([0,\infty)\) 區間上就有反函數,它是 \(x\mapsto\sqrt{x}\),如右圖。



其實 \(y=f(x)\) 的圖形就是 \(x=f^{-1}(y)\) 的圖形。 例如 \(y=e^x\) 等價於 \(x=\ln y\),它們的圖形是同一條曲線,如以下左圖。
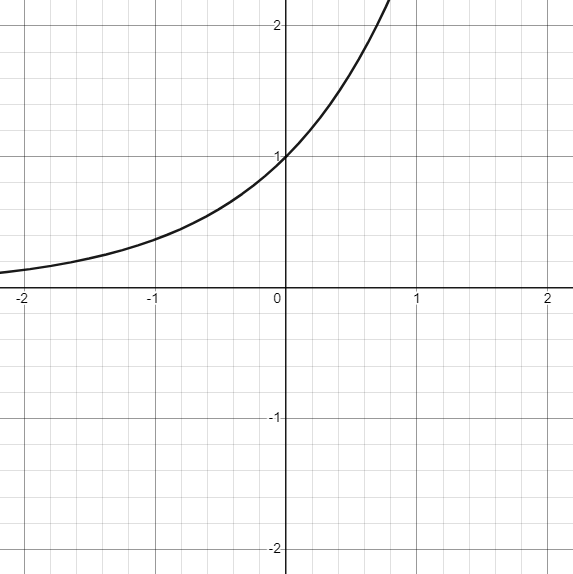
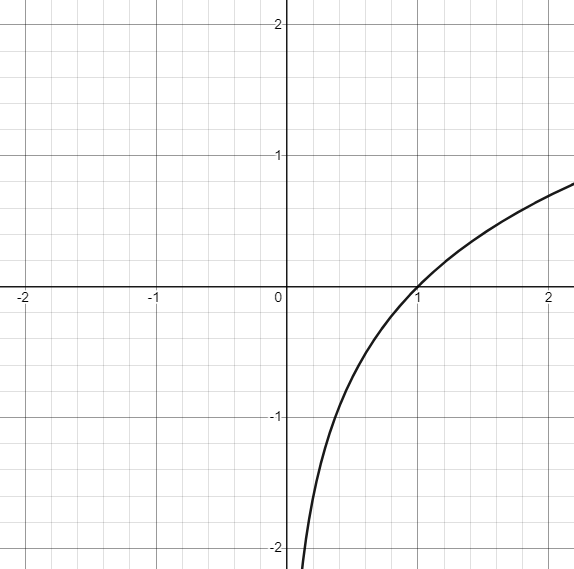
因為 \((x,y)\) 與 \((y,x)\) 兩點對稱於 \(y=x\) 直線, 所以對調 \(x\) 與 \(y\) 的效果,就是圖形對稱於 \(y=x\) 直線。 也就是說函數 \(f\) 與其反函數 \(f^{-1}\) 的圖形對稱於 \(y=x\) 直線。
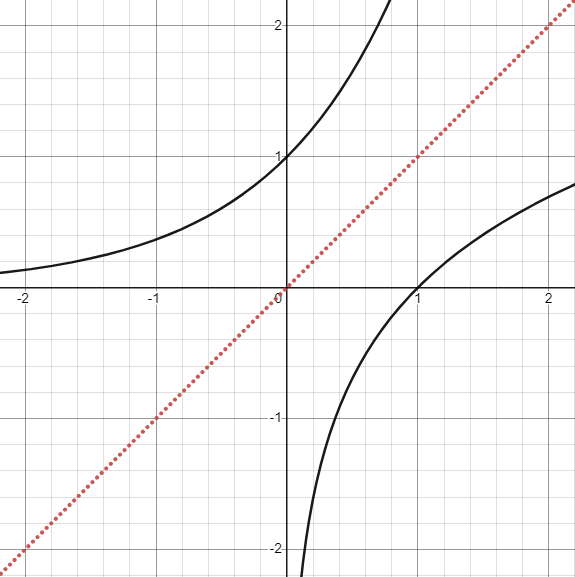
The graphs of inverse functions are symmetric about the line \(y=x\).例如 \(x\mapsto e^x\) 和 \(x\mapsto \ln x\) 互為反函數, 而 \(e^x\) 和 \(\ln x\) 的函數圖形對稱於 \(y=x\) 直線,如下圖。
| [語音講解:invfcn.mp3] |