數學英文

機率樹

當事件 \(A\) 和 \(B\) 彼此獨立時，它們的積事件──\(A\) and \(B\)──發生的機率可以用特殊的機率乘法律來計算，也就是 \(P(A\text{ and }B)=P(A)\times P(B)\)。但這條公式只是特例。

機率乘法律的一般情況需要另一種機率概念：條件機率 (conditional probability)， 記作 \(P(A\mid B)\)，意思是在已知 \(B\) 發生的條件下，\(A\) 的機率： The probability of \(A\) under the condition that event \(B\) has occurred， 可以簡單讀作 the probability of A given B， 或者更簡化為 P of A given B。 事件 \(A\) 與 \(B\) 彼此獨立就相當於 \(P(A\mid B)=P(A)\)， 或者 \(P(B\mid A)=P(B)\)，這兩條等式是等價的：它們要不同時成立，要不同時不成立。 所以

• 機率乘法律的一般情況就是 \[P(A\text{ and }B)=P(A\mid B)\times P(B)\]

在西方的教學脈絡中（香港、新加坡也是），條件機率 \(P(A\mid B)\) 是在情境中算出來的（例如取出不放回的情境），用它來計算 \(P(A\text{ and }B)\)。 我國的教學脈絡，習慣用集合關係先計算 \(P(A\cap B)\)，然後用它來定義 \(P(A\mid B)\)。在邏輯上，兩種脈絡殊途同歸，但是在學習經驗上， 西方的脈絡比較能彰顯學習機率的有用之處。

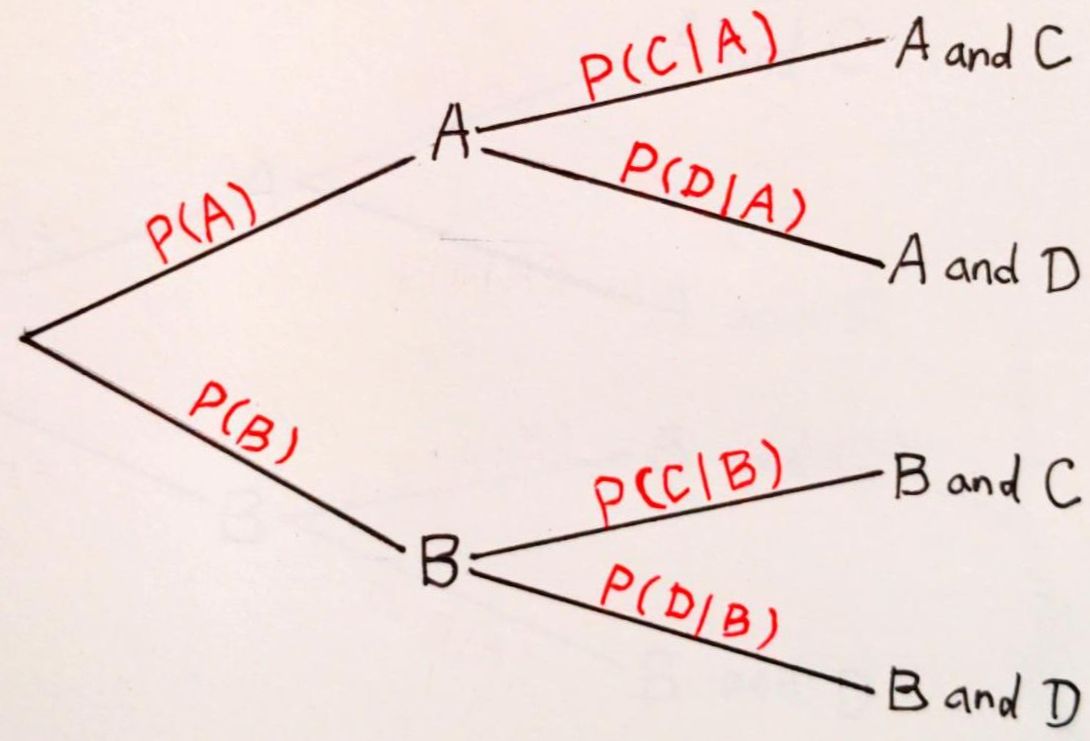
機率樹狀圖 (probability tree diagram) 特別適合用來協助處理機率的加法律與乘法律。 機率樹狀圖的節點 (nodes) 表示事件，而樹枝 (branches) 記錄它發生的機率， 參閱以下圖示，直行的事件是互斥的「或」，橫向沿著樹枝的事件是「且」， 所以直行的機率可以相加，而沿著樹枝的機率要相乘。 至於橫向事件是獨立或相依，例如 \(A\) 和 \(C\) 是獨立或相依，並不重要， 反正一般而言那條樹枝上面就記錄 \(P(C\mid A)\)。 如果 \(A\) 和 \(C\) 彼此獨立，自然就 \(P(C\mid A)=P(C)\)； 而不論如何，事件「\(A\) and \(C\)」的機率就是沿著樹枝把機率乘起來： \[P(A\text{ and }C)=P(A)\cdot P(C\mid A)\]