平行性 (parallelism) 雖然是刻畫歐氏幾何的關鍵特徵， 但是證諸於後來的發展與應用，其實正交性 (orthogonality) 更為重要， 反而平行可以視為垂直的推論與應用。 正交 (orthogonal) 是垂直 (perpendicular) 的同義詞（皆為形容詞）。
平行線 (parallel lines) 的意思是同平面且永不相交的直線：
Lines lying in the same plane but never meeting in either direction.所以空間中的平行線一定要共面且無交點：
coplanar straight lines that do not intersect at any point空間中不共面的直線當然也不相交（因為兩相交直線決定一平面）， 它們稱為歪斜線：
Two noncoplanar lines are called skew lines.
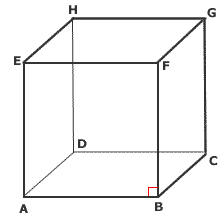空間中直線關係的基本模型可參照立方體的稜，如右圖，以直線 \(AB\) 為例：
歐氏幾何的公設系統需要用設準 (postulate) 來保證可作線外一點的平行線：
to construct a line parallel to a given line through a given point但學校數學因為先認識了垂直，而且早就建立了三角形內角和定理， 所以可以用兩條垂線作平行線，而（平面上）垂線的唯一性則在操作中默認。 由此可以推論，平行線的特徵──也就是兩條直線彼此平行的充分必要條件 (necessary and sufficient condition) 是它們有公垂線 (common perpendicular)。
兩直線 \(L\) 與 \(M\) 平行的符號是 \(L\parallel M\) 或 \(L\,\text{/}\!\!\text{/}\,M\)。 平行線之間的距離 (distance between two parallel lines) 即公垂線段的長度 (length of the perpendicular segment between them)， 也就是任一條公垂線與兩條平行線之交點的距離：
The distance between two points of intersection of the parallel lines and a common perpendicular.
公垂線是截線 (transversal) 的特例， 截線是指兩條平行線以外的第三條直線，它與兩平行線各交於一點； 當然，這三條直線在同一平面上。
A transversal is a line that passes through two parallel lines at two points.截線與兩條平行線形成 8 個角，組成 12 雙成對的角（對頂角不算）：
不相交的平面叫做平行面 (parallel planes)，空間中不相交的直線與平面也稱為平行； 例如，參照前面的立方體視圖， 頂面 (top) 的對角線 \(HF\) 平行於底面 (base) \(ABCD\)。
| [語音講解：parallel.mp3] |