機率論(probability theory)的濫觴, 是一位法國貴族在大約 1652 年給巴斯卡(Blaise Pascal, 1623--62)的一個提問。 他文雅地說明一個「機會賽局」(game of chance)--其實就是賭博 (gambling) ──的規則,提問是:如果賭博中斷,如何根據現狀「公平地」分配彩金 (prize) 或賭金 (stakes)? 這個了不起的「機率史上第一題」甚至有了自己的名字:the Problem of Points。 因為最終的目的是根據理論上的機率來分配彩金,所以它其實是期望值問題 (expectation 或 expected value)。
巴斯卡顯然很滿意自己提出的解決方案,他在 1654 年為此寫了一本小書: Traité du triangle arithmétique,英文的意思是 Treatise on Arithmetic Triangle,《算術三角論》; 可是在他身後三年 1665 年才出版。
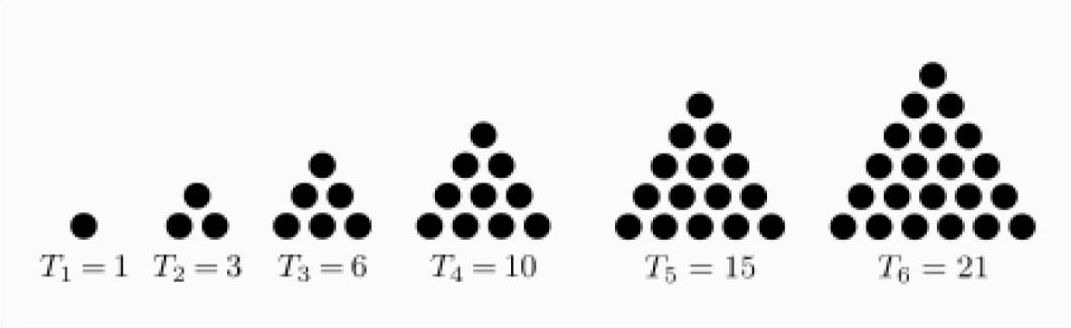
他所謂的「算術三角」就是我們如今說的巴斯卡三角,或者稱楊輝三角、賈憲三角。 別跟「三角數」搞混了,所謂 triangle number 或 triangular number 是指 1, 3, 6, 10, 15, 21, ... 這些數。

在巴斯卡三角的每一橫列 (row) 上,是二項式展開 (binomial expansion) 的係數, 也就是二項式係數(binomial coefficients)。 這些數同時也是組合學(combinatorics)或組合數學(combinatorial mathematics) 的組合數(combinations 或 combination number), 在高中習慣記作 \(C^n_k\),但是在專業數學通常記作 \(\displaystyle{n\choose k}\), 它們的意思都是 the combination number of choosing k from n, 讀作 n choose k,而 \(C^n_k\) 可以簡讀作 C n k,其中 C 代表 choose。 巴斯卡發現的「算術三角」一般項公式 (general term formula): \[C^n_k ={n(n-1)(n-2)\cdots(n-k+1)\over 1\cdot 2\cdot 3\cdots k}\] 如今經常用來當作組合數定義。
Pascal 用他的「Arithmetic Triangle」來回答 Problem of Points。 假如賭金是 \(P\),則「公平的」分配是:其中一人取得 \[{R\over 2^n}\times P\] 其中 \(R\) 是巴斯卡三角第 \(n\) 列前 \(k\) 項的和,也就是 \[{C^n_0+C^n_1+\cdots+C^n_{k-1}\over 2^n}\times P\] 當然 \(k\leq n\)(k is not greater than n),而另一人取得剩下的賭金。 以上 n 和 k 的意義,請看:
蘇惠玉(2018)。追本數源。臺北市:三民。(篇 9)
| [語音講解:pascal.mp3] |