
空間的關鍵概念在於直線與平面的垂直性 (perpendicularity)。 所謂「直線垂直於平面」(a line is perpendicular to a plane) 的定義 (definition) 是, 直線與平面交於一點(稱為 foot),且該直線與平面上通過垂足的所有直線皆垂直:
the line is perpendicular to every line in the plane that passes through its foot「垂直」是互相的,當直線垂直於平面,反過來也說平面垂直於直線:
When a line is perpendicular to a plane, the plane is also said to be perpendicular to the line.在此定義之下,給定一點與一平面,可作通過該點而垂直於平面的直線:
Given a point and a plane, through the point pass a line perpendicular to the plane.像這樣的直線是唯一的。
垂直於平面的直線又稱為平面的「法線」,英文的正式對譯為 normal line。 但是,英文說 normal line 時,通常是指垂直於某條曲線之切線的直線, 在空間幾何的語境中,英文通常還是說 the line perpendicular to a plane。
所謂「法線定理」(Line-Plane Perpendicularity Theorem) 是說, 只要直線垂直於平面上通過垂足的任兩條(相異)直線,它就垂直於整個平面:
If a line is perpendicular to two different lines that lie in a plane and pass through its foot, then it's perpendicular to the plane.用兩片三角板就能實驗法線定理的意義。
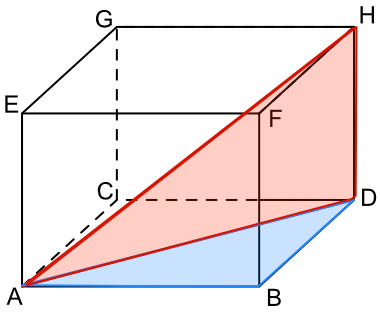
長方體是空間中直線與平面關係的最基本舞台。 設右圖是一個長方體,則稜 HD 垂直於底面的兩個邊 CD 和 BD, 所以(根據法線定理)稜 HD 垂直於底面,也就是直線 HD 是底面 ABCD 的法線, 垂足 (foot) 為點 D。 那麼,根據垂直的定義,HD 垂直於底面上通過 D 點的任何直線; 譬如三角形 ADH 是直角三角形。
換個角度來看,直線 AB 是右側面 HDBF 的法線, 三角形 BDH 是側面上的一個直角三角形, 則將 BDH 的頂點 B 在法線上任意移動所得的三角形,皆為直角三角形; 譬如三角形 ADH 是直角三角形。 這是所謂的「三垂線定理」(Theorem of Three Perpendiculars):
如果平面上有一個直角 \(\triangle\)ABC,其中 \(\angle\)C 是直角, 讓頂點 A 沿著法線上升或下降到另一點 A\({}^\prime\), 則空間中的 \(\triangle\)A\({}^\prime\)BC 還是一個直角三角形。
所謂「三垂線」是指定理中作為前提條件 (the premise) 的三條直線,
它們之間在兩張互相垂直的平面上形成兩個直角;
譬如上圖的「三垂線」是 AB、BD、DH,其中 AB 和 BD 在底面形成直角、
BD 和 DH 在右側面形成直角。
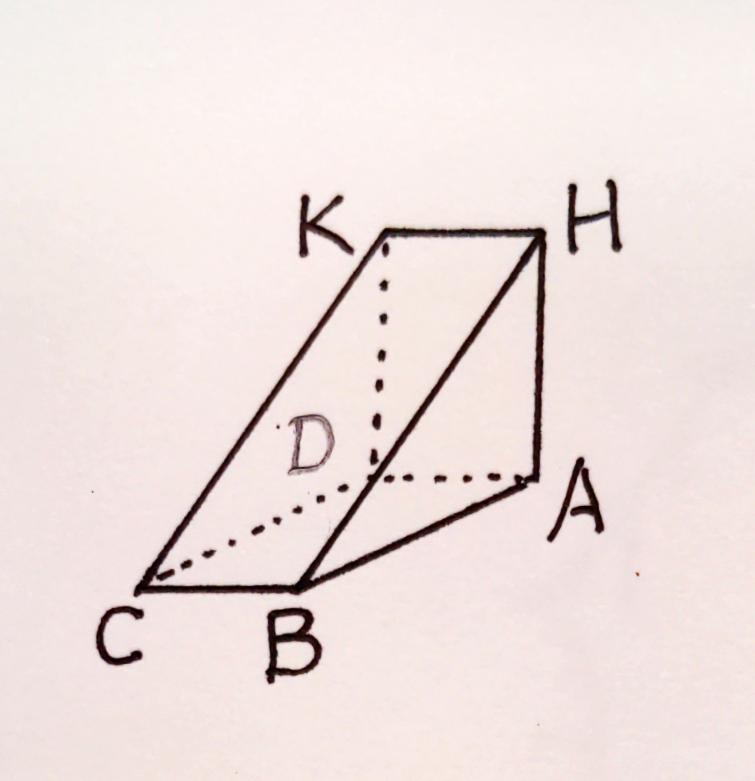 右圖是另一個三垂線定理的常見配置:
在三明治的斜面上,想要證明 \(\angle\)CBH 是直角。
其實三明治就是三稜鏡,也就是三角柱,通常它的三角形的面是等腰直角三角形。
在生活經驗中,我們知道三明治的斜面 CBHK 是長方形,所以 \(\angle\)CBH 當然是直角,但數學老師用三垂線定理來證明這個簡單的事實。
這裡的「三垂線」是:
右圖是另一個三垂線定理的常見配置:
在三明治的斜面上,想要證明 \(\angle\)CBH 是直角。
其實三明治就是三稜鏡,也就是三角柱,通常它的三角形的面是等腰直角三角形。
在生活經驗中,我們知道三明治的斜面 CBHK 是長方形,所以 \(\angle\)CBH 當然是直角,但數學老師用三垂線定理來證明這個簡單的事實。
這裡的「三垂線」是:
HA、AB,和 CB
同樣的結論也可以直接從法線定理獲得。 首先,三點 B, A, H 決定一平面,而 CB 是它的法線(把三明治放進一個外接長方體就看出來了),而 BH 是右側面上通過垂足 B 的直線,所以 CB \(\perp\) BH。 符號 \(\perp\) 唸「垂直於」或 perp,是 perpendicular 的縮寫。
| [語音講解:plane.mp3] |