有規則的多面體，基本形式是錐體 (pyramids) 和柱狀體 (prismatoid)。
錐體有一個特殊的頂點，稱為 apex，其他頂點都落在同一平面上，那張平面稱為底面 (base)，柱狀體則有互相平行的底面和頂面，所有頂點都落在這兩張平面上（而且都多於一點）。
利用截角 (truncation)，可以從基本多面體創造新的多面體；
截角的意思是切掉一個頂點而產生新的面：
自然界的形體 (solids) 當然多得數不清，人類創造的形體則可以粗分兩大類： 多面體 (polyhedra) 和旋轉體。 形體都是有凸有凹的 (convex / concave)，沒有特別聲明時， 多面體是指凸多面體 (convex polyhedra)。
有規則的多面體，基本形式是錐體 (pyramids) 和柱狀體 (prismatoid)。
錐體有一個特殊的頂點，稱為 apex，其他頂點都落在同一平面上，那張平面稱為底面 (base)，柱狀體則有互相平行的底面和頂面，所有頂點都落在這兩張平面上（而且都多於一點）。
利用截角 (truncation)，可以從基本多面體創造新的多面體；
截角的意思是切掉一個頂點而產生新的面：
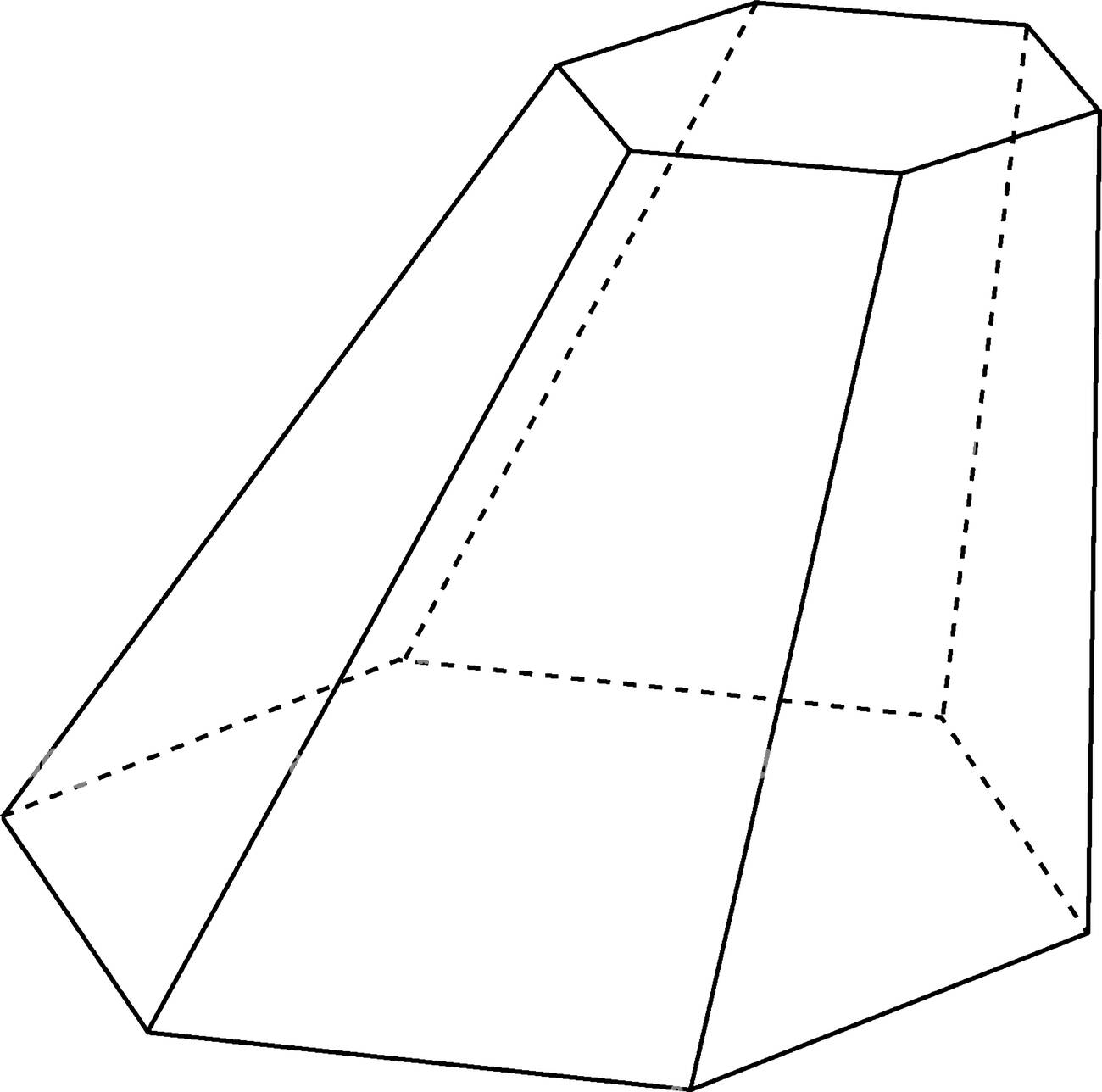
cut a vertex and create a new facet in place of the vertex例如角錐臺 (frustum，複數 frusta) 是截掉角錐體的 apex 而得的多面體，如右圖。
由四邊形的面組成的六面體 (quadrilateral-faced hexahedra) 可能是最常見的柱狀物。除了立方體 (cube) 和長方體 (cuboid) 以外， 還有平行六面體 (parallelepipeds)； 其中六邊等長（也就是六個面皆為菱形）的平行六面體，稱為 rhombohedron（菱面體）。
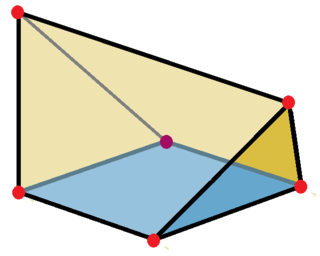三角柱（三稜鏡）是五面體 (pentahedron) 的基本形式，
將它的長方形的面變形為梯形之後，通稱為楔形 (wedge)；
也就是楔形有兩個三角形的面，三個梯形的面，如右圖。
Wedges are pentahedra with two triangular and three trapezoidal faces.
正多面體 (regular polyhedron) 的定義是所有面皆為彼此全等的正多邊形：
the faces are congruent regular polygons不像正多邊形可以有任意多邊，（凸）正多面體卻只有五種， 它們又稱為柏拉圖多面體 (Platonic solids)： 正四面體 (tetrahedron)、立方體、正八面體 (octahedron)、正十二面體 (dodecahedron)、正二十面體 (icosahedron)。
把正多面體的定義放寬一點：每個面皆為正多邊形，但不要求彼此全等，
則稱為半正規多面體 (semiregular polyhedron)，這樣就會多一些種類，
包括阿基米德多面體 (Archimedean solids)。
例如右圖是由截角立方體 (truncated cube) 得到的一種阿基米德多面體；
它的每個面都是正三角形或正八邊形。
關於形體的計算，無非就是算體積 (volume) 與表面積 (surface area)； 基本形體都已經有體積與表面積的公式 (formula，複數是 formulas 或 formulae)。 錐體都有明顯的底面，柱狀體則要約定底面──確定了柱狀體的底面之後，它的頂面 (top) 也跟著確定了。 除了底面和頂面以外的所有面，都稱為側面 (lateral faces)。 所謂側面積 (lateral area) 就是側面的面積， 也就是扣除底面和頂面（如果有）的表面積。
| [語音講解：polyhedron.mp3] |