數學英文

四邊形

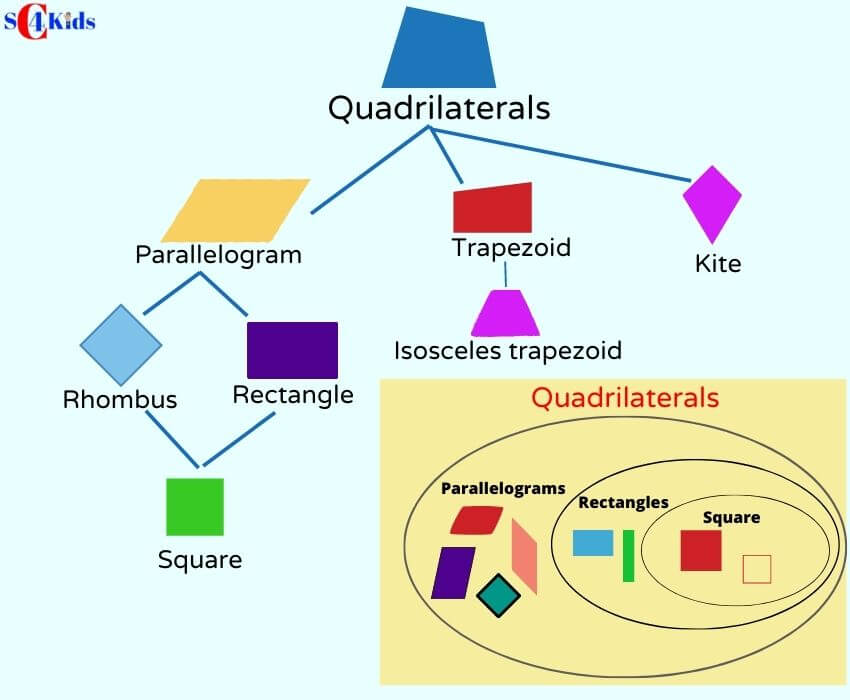
四邊形集合關係的樹狀圖及文氏圖。

人造物體的表面常常是四邊形，工業與商品設計也經常利用四邊形。 臺灣的數學課程，通常只是把四邊形用來鍛鍊邏輯推理 (logical inference)。 西方的課程裡，四邊形通常還有平面拼貼 (tessellation 或 tiling) 的應用課題。

四邊形可以作為鍛鍊邏輯的工具，是因為各種特殊四邊形之間有較為複雜的從屬關係， 一圖以蔽之：

• Quadrilaterals，四邊形，指一般的、無特殊規則的四邊形
• Parallelogram，平行四邊形，注意 parallel 就是平行的意思；它的特徵：
  • One pair of opposite sides are parallel and equal（一組對邊平行且相等）
  • Opposite sides are equal（兩組對邊分別相等）
  • Opposite angles are equal（兩組對角分別相等）
  • Diagonals bisect each other（對角線互相平分）
• Rectangle，長方形、矩形，具備平行四邊形所有特徵，並且
  • All angles are equal（四個角皆相等，皆為直角；其實只要一個角為直角即可推論四個角皆為直角）
• Rhombus（複數是 rhombi），菱形，具備平行四邊形所有特徵，並且
  • All sides are equal（四個邊皆相等）
  • Diagonals are perpendicular（對角線互相垂直；因為它們本來就互相平分，所以其實是互相垂直平分）
  • Diagonal bisects a pair of opposite angles（對角線亦為角平分線）
• Square 正方形，同時具備矩形與菱形的特徵：四邊皆相等的長方形，或者四角皆相等的菱形。
• Trapezoid / trapezium，梯形：恰有一組對邊平行（exactly one pair of parallel sides），這兩邊都稱為底 (bases)，必要時可分上底 (top) 和下底 (base)。
• Isosceles trapezoid，等腰梯形：梯形中不平行的兩邊（稱為 legs）等長 (legs are congruent 或 legs are of equal length)。 還有以下特徵：
  • Base angles are equal（底角相等；有兩組底角，它們互為補角）
  • Diagonals are equal（對角線等長）
• Kite，箏形：
  • Two pairs of adjacent sides are equal（兩組鄰邊相等）
  • One pair of opposite angles is equal（一組對角相等）
  • Diagonals intersect at right angles（對角線垂直）
  • One diagonal bisects the other diagonal（某對角線平分另一條對角線，其實某對角線是另一條對角線的中垂線）

在平行四邊形與梯形中，一組平行對邊的距離就稱為「高」(height)， 而他們的面積原則上就是底乘以高（梯形的面積是兩底的平均值乘以高）。 當對角線互相垂直時（箏形、菱形、正方形），面積是對角線相乘的一半 (half the product of the lengths of diagonals)。

長方形的兩組對邊，在數學課裡的名稱是長、寬； 有時候說比較長的邊為長 (length)，比較短的邊為寬 (width)， 也有些時候說水平的邊 (horizontal side) 為寬，鉛直的邊 (vertical side) 為長。 在生活中，鉛直的邊也會稱為高 (height)。