




自然界的形體 (solids) 當然多得數不清,人類創造的形體則可以粗分兩大類: 多面體和旋轉體 (solids of revolution)。 形體都是有凹凸性 (convexity),多面體通常默認為凸的,但旋轉體並不這樣默認。
生活中有許多器物是以旋轉的方式製造的,例如陶器是在歷史悠久的轆轤 (pottery wheel) 上塑造它的形狀,也就是拉胚 (wheel-throwing),如右圖。 工廠裡的車床 (lathe) 與銑床 (milling machine) 都是製造旋轉體的工具。
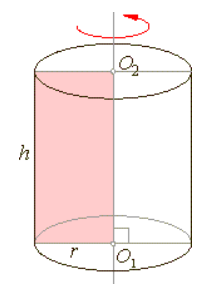
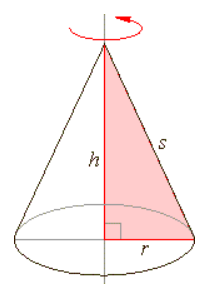
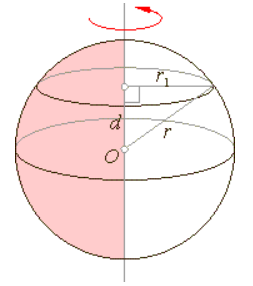
數學上,旋轉體是給定一個平面圖形(封閉區域:closed region)與同平面上一條直線, 原則上直線不穿越圖形(直線可以在圖形的邊界上), 則圖形在空間中繞直線旋轉而成的立體稱為旋轉體。 在此情境中,不計較旋轉超過一圈的重複部份。 前述直線稱為旋轉軸 (axis of revolution)。 下圖顯示長方形旋轉成圓柱體 (cylinder)、直角三角形旋轉成圓錐體 (cone)、 半圓形 (semicircular disk) 旋轉成球 (sphere) 的示意。
圓柱與圓錐除了底面/頂面以外的曲面,稱為側面; 注意英文說多面體的側面是 lateral faces,圓柱與圓錐的側面是 lateral surface, 但中文都說「側面」,所以要注意圓柱和圓錐的側面並非平面。 旋轉體的側面積 (lateral area) 是指它的 lateral surface 的面積。 圓柱和圓錐的側面都可以展開成平面圖形, 圓柱側面的展開圖 (the net) 是長方形,圓錐側面的展開圖是扇形 (circular sector)。
旋轉成圓柱或圓錐的側面的那條線段稱為母線 (generatrix 或 generating line 意思就是「產生圓柱或圓錐的線」), 而它們底部的圓(周)稱為 directrix; 其實 directrix 可以從圓推廣為任意封閉曲線,例如橢圓; 當然,那樣製造出來的柱體和錐體就不是旋轉體了。 注意,在圓錐曲線的語境中,directrix 翻譯為準線, 但是在旋轉體的語境中, 比較適合稱為導線:導引一條直線段形成柱體或錐體的封閉曲線。 圓錐體的母線長,俗稱為斜高 (slant height)。
旋轉體垂直於旋轉軸的橫剖面 (cross sections) 皆為圓盤 (disk) 或圓環 (正式名詞是 annulus,俗稱 circular ring 或 washer)。
類似於旋轉體,旋轉一段曲線可以在空間中形成旋轉曲面 (surface of revolution)。 旋轉體的側面都可以視為旋轉曲面。
旋轉體的體積與表面積、側面積都有公式 (formulae)。 最精彩的是帕普斯形心定理 (Pappus centroid theorem), 它斷言:當旋轉軸不通過平面圖形內部時,旋轉體的體積是平面圖形的面積乘以它的形心旋轉之後的圓周長:
The volume of the solid obtained by revolving a plane region D about the axis L not intersecting D is the product of the area of D and the length of the circular path traversed by the centroid of D.
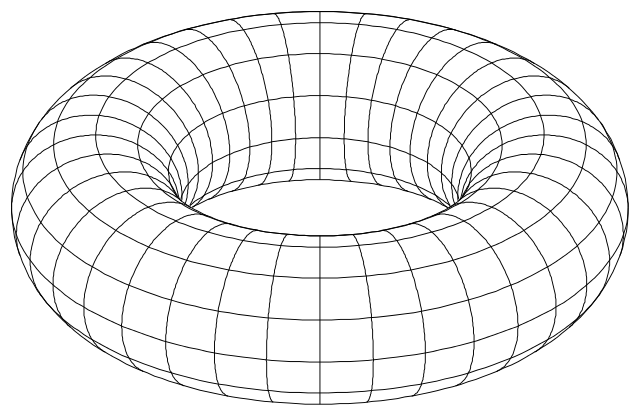 例如在平面上給定一直線 L 與圓 C,令圓半徑為 \(a\),
圓心至直線的距離為 \(b\),其中 \(a<b\),則圓 C 繞直線 L 旋轉所成的 torus
(輪胎或甜甜圈),如右圖,體積為(圓的形心就是圓心)
\[(\pi a^2)\times (2\pi b) = 2\pi^2a^2b\]
例如在平面上給定一直線 L 與圓 C,令圓半徑為 \(a\),
圓心至直線的距離為 \(b\),其中 \(a<b\),則圓 C 繞直線 L 旋轉所成的 torus
(輪胎或甜甜圈),如右圖,體積為(圓的形心就是圓心)
\[(\pi a^2)\times (2\pi b) = 2\pi^2a^2b\]
| [語音講解:revolution.mp3] |