
我們到文具行買一個三角板──它的英文商品名稱就是 triangle──買來的就是一個直角三角形 (right triangle) 的板子。 可見直角三角形是最實用的三角形。 三角形的各種性質在直角三角形上也都成立,而且更容易理解(例如內角和定理); 反過來看,許多三角形的性質,可以視為直角三角形性質的推廣, 例如面積公式、正弦定理、餘弦定理。
直角三角形的斜邊,中文稱「弦」,英文是 hypotenuse,來自希臘文。 弦以外的兩邊稱為兩股 (two legs), 所以
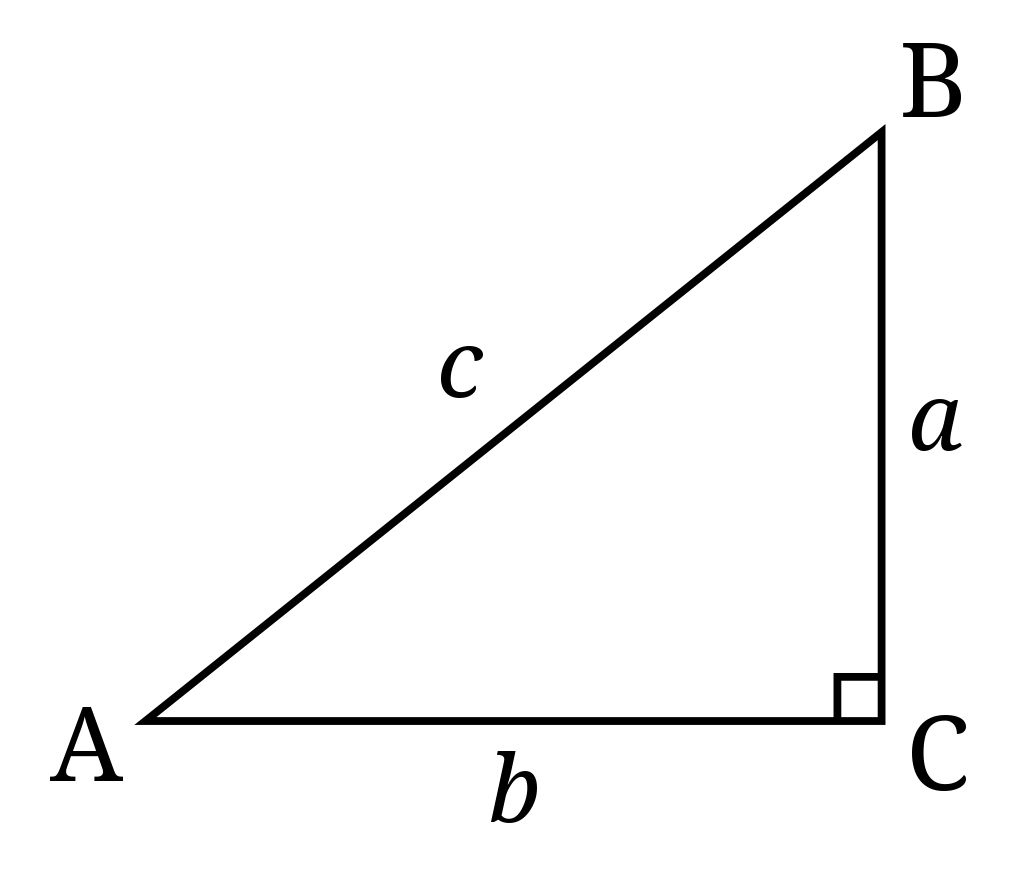
A right triangle has two legs.將三角形「擺正」之後,如右圖,legs 有「勾股」之分:勾是底 (base),股是高 (perpendicular 或 height)。 我們習慣用 \(a\), \(b\), \(c\) 表示邊和邊長, 用 \(A\), \(B\), \(C\) 表示頂點和其內角, 而 \(a\) 邊是角 \(A\) 的對邊:Side \(a\) is the side opposite angle \(A\)。 斜邊是直角的對邊:The hypotenuse is the side opposite the right angle。
直角三角形有兩個最深刻的性質,第一個是:
這個定理被譽為人類的第一個數學定理。
斜邊平方等於兩股平方和。
The square of the hypotenuse is equal to the sum of the squares of the legs.
| [語音講解:rightriangle.mp3] |