


相似形 (similar figures) 在日常語言中的意思是 「形狀相同但大小不見得相等」的圖形:
Figures having the same shape, but not necessarily the same size.此觀念來自:以同一視角 (viewpoint) 在不同距離觀看同一物件的視覺經驗。



若想要用數學語言定義相似形,則只能定義幾何形體之間的「相似性」(similarity)。 最基本的相似概念是矩形 (rectangles) 的相似性: 當矩形的長寬比 (length-to-width ratio / aspect ratio) 是等比 (相等的比,equivalent ratios) 時,它們彼此相似 (they are similar); 例如下圖左側、中間兩個矩形相似,它們與右側矩形不相似: 前者是 16:9 的矩形 (sixteen to nine),後者是 4:3 (four to three)。



若將兩個相似的長方形 \(ABCD\) 和 \(AB^\prime C^\prime D^\prime\) 沿左下角對齊: 令頂點 \(A\) 在左下角,點 \(B^\prime\) 在 \(AB\) 直線上, 點 \(D^\prime\) 在 \(AD\) 直線上, 則它們的對角線 \(AC\) 和 \(AC^\prime\) 延伸成同一條直線, 也就是點 \(C^\prime\) 一定落在直線 \(AC\) 上。
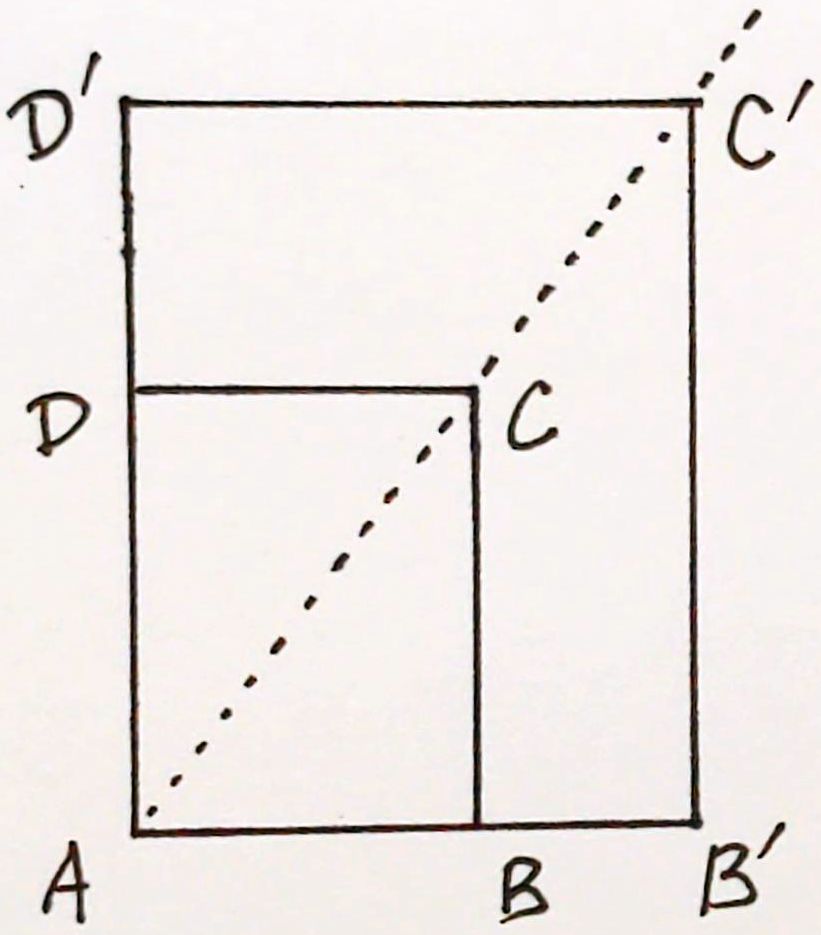
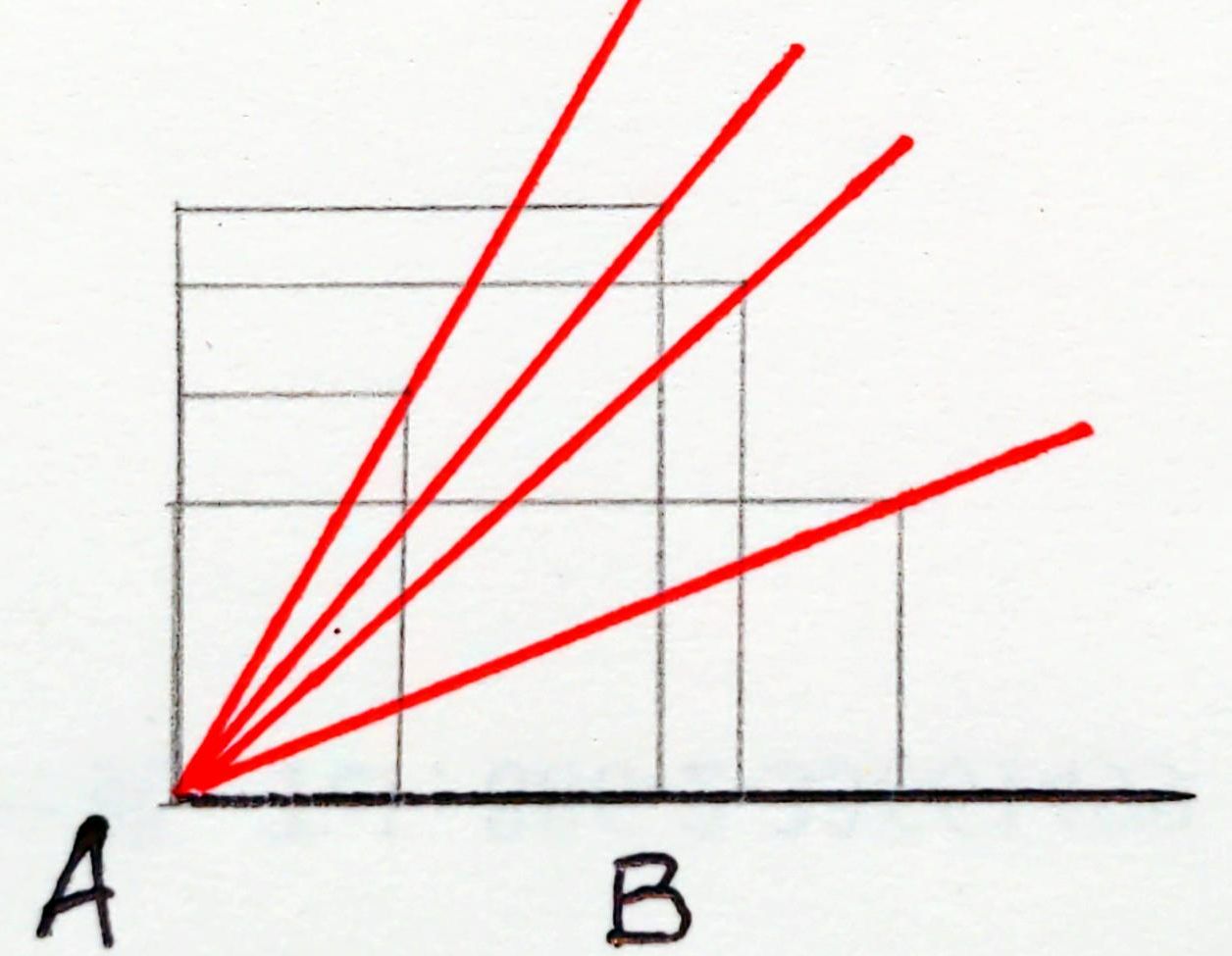
從矩形的相似性可定義相似的直角三角形,並可推論: 兩股成比例的直角三角形彼此相似;再進一步發現:兩股的比值可以決定一個銳角。 這是因為,如果把長方形的底邊和左邊對齊, 觀察它們的對角線,可以看到不同比值的長方形決定不同的對角線。 於是這些對角線和底邊所夾的角,就跟長方形的兩邊比值,有了一一對應的關係。
用「正切表」(tangent table) 可檢索兩股比值與對應銳角的角度。 對一般人而言,「正切表」就像算盤和輪胎似的,屬於文化遺產 (cultural heritage); 它怎麼來的暫時並不重要,重要的是學會用它。
從直角三角形的相似性,可推論:兩組對應角相等的三角形彼此相似, 它們的對應邊成比例:
Two triangles are similar if there are two congruent corresponding angles, their corresponding sides are in proportion.三角形只要對應角相等就相似了,也就是三角形的對應角相等可保證對應邊成比例; 但是長方形並非如此:長方形的對應角皆相等(都是直角),但是如果對應邊不成比例,就不是相似長方形。 推廣至一般的多邊形,當對應角相等而且對應邊成比例時,它們是相似多邊形。
當邊數 \(n\geq 3\) 時,正 \(n\) 邊形 (regular \(n\)-gons) 彼此相似。 所有圓彼此相似:All circles are similar to each other; 所有球也彼此相似。
| [語音講解:similar.mp3] |