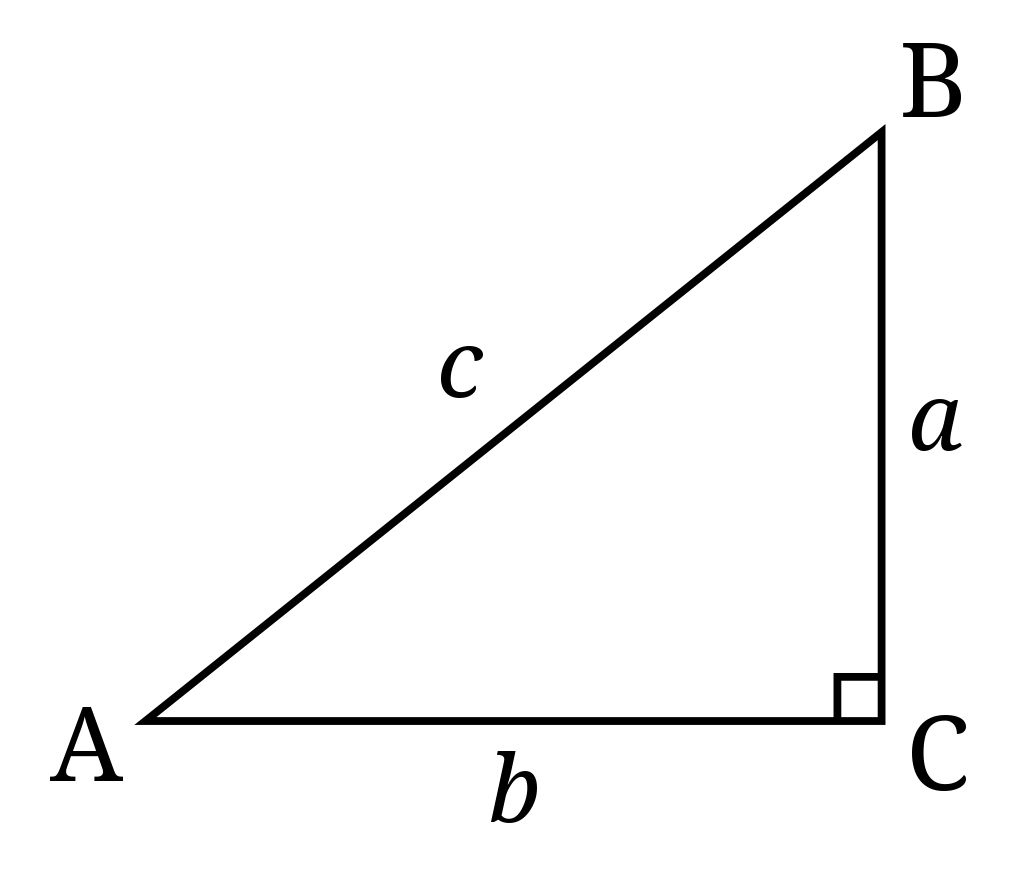

直角三角形的第二個深刻性質是
只要指定任一銳角(就說是 \(\angle A\),say \(\angle A\)), 則所有這樣的直角 \(\triangle ABC\) 皆彼此相似 (similar), 因此 \(a:b:c\) 是一個固定的比。 如果我們定義 \[a:b:c = \sin A:\sin B:1\] 再規定 \(\sin90^\circ:=1\), 則所謂「正弦定理」(Law of Sines) 在直角三角形上僅為正弦 (sine) 的定義, 然後它可以推廣到一般三角形。
餘弦 (cosine) 定義為餘角的正弦 (sine of the complementary angle), 亦即 \(\cos A=\sin(90^\circ-A)\)。 所謂「餘弦定理」(Law of Cosine,又稱為 cosine formula 或 cosine rule) 可以視為畢氏定理在斜三角形上的推廣: an extension / generalization of the Pythagorean theorem on non-right triangles。 當 \(\angle C\) 是鈍角,邊長 \(c\) 的平方大於 \(a^2+b^2\), 它的修正項 (correction term) 是加上 \(2ab\cos C^s\): \[c^2 = a^2 + b^2 + 2ab\cos C^s\] 其中 \(C^s\) 表示 \(\angle C\) 的補角(supplementary angle of C,\(180^\circ-C\))。 這其實是《幾何原本》(Elements) 第二卷命題 12 (Book 2, Proposition 12), 原文寫著:
In obtuse-angled triangles, the square on the side subtending the obtuse angle is greater than the (sum of the) squares on the sides containing the obtuse angle by twice the ...意思是說「在鈍角三角形裡,鈍角的對邊平方比鈍角的兩邊平方和多了...」, 而多出來的量就是 \(2ab\cos C^s\)。 只不過當年還沒有 \(\cos\) 觀念,所以算法較複雜。
當 \(\angle C\) 是銳角,邊長 \(c\) 的平方小於 \(a^2+b^2\), 修正項要減去 \(2ab\cos C\): \[c^2 = a^2 + b^2 - 2ab\cos C\] 這是《幾何原本》第二卷命題 13 (Book 2, Proposition 13)。
我們只要規定 \(\cos90^\circ:=0\),畢氏定理就成了餘弦定理的特例, 也就是當 \(\angle C\) 是直角時,修正項等於 0。
對大眾而言,任意銳角的三角比(sine 和 cosine)都可以當作已知, 只要用計算機就能查到它的近似值。它們的值怎麼來的暫時不重要, 就像語言和數目字一樣,它們就是文化遺產 (cultural heritage): 學會使用它們才重要。
| [語音講解:sine.mp3] |