數學英文

三角形

三角形 (triangle) 是最少邊數的多邊形。 在邏輯上，三角形是最基本的平面圖形，可是四邊形才是人們生活經驗中最熟悉的圖形。 四邊形可以沿對角線分割成兩個三角形； 反過來，每個三角形都是某個平行四邊形沿對角線分割的一半， 所以它的面積是二分之底乘以高。

三角形可以細分為幾個種類，按照它們在應用上的重要程度，依序為：

• 直角三角形：Right-angled triangle 或 right triangle。
• 等腰三角形：Isosceles triangle，其中
  • 兩腰的英文是 legs，第三邊稱為底 base。
  • 兩腰的對角稱為底角，底角相等：Two angles opposite the legs (base angles) are equal.
  • 兩腰的夾角稱為頂角 (vertex angle 或 apex angle)；頂角可能為銳角、直角或鈍角，但底角必為銳角。頂角的頂點稱為 apex。
  • 底的中線 (median to the base 或者說 median from the apex，即頂點與底邊中點決定的直線）是等腰三角形的對稱軸 (axis of symmetry)； 此中線是頂角的角平分線 (the angle bisector of the vertex angle)， 也是底的中垂線 (the perpendicular bisector of the base)。
• 等邊三角形：Equilateral triangle，又稱為正三角形 (regular triangle)。
  • 有時候將正三角形視為等腰三角形的特例，有時候規定正三角形並非等腰三角形，這件事並無全球的共識，要注意個別文件的前提。
• 銳角三角形：Acute-angled triangle（三角皆為銳角）。
• 鈍角三角形：Obtuse-angled triangle（某一角為鈍角）。
• 斜三角形：Oblique triangle（非直角三角形，銳角或鈍角三角形）又稱 non-right triangle。
• 不規則三角形：Scalene triangle（又稱為不等邊三角形，三邊不互等，可推論三角亦不互等）。

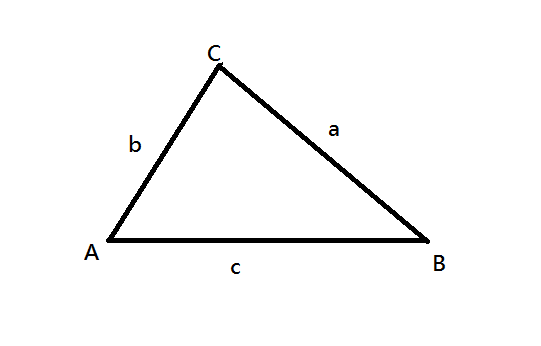我們習慣用 \(A\), \(B\), \(C\) 表示三角形的頂點， 記作 \(\triangle ABC\)，讀作「三角形 ABC」(Triangle ABC)。 我們同時也用 \(A\), \(B\), \(C\) 表示內角， 例如頂點 \(A\) 的內角記作 \(\angle A\)， 讀作「角 A」(angle A)。 我們用 \(a\), \(b\), \(c\) 同時表示邊和邊長， 而 \(a\) 邊是角 \(A\) 的對邊：Side \(a\) is the side opposite angle \(A\)。

沒有特別聲明時，三角形的「角」是指內角 (interior angles)。 三角形的內角和定理 (angle sum theorem for triangles) 斷言三個角加在一起等於一個平角（俗稱 180 度）：

Sum of all the interior angles of a triangle is equal to a straight angle.

The exterior angle of a triangle is equal to the sum of the / two remote / opposite interior angles.

因為空間中不共線三點決定一平面， 所以空間中的三角形必然落在同一平面上。