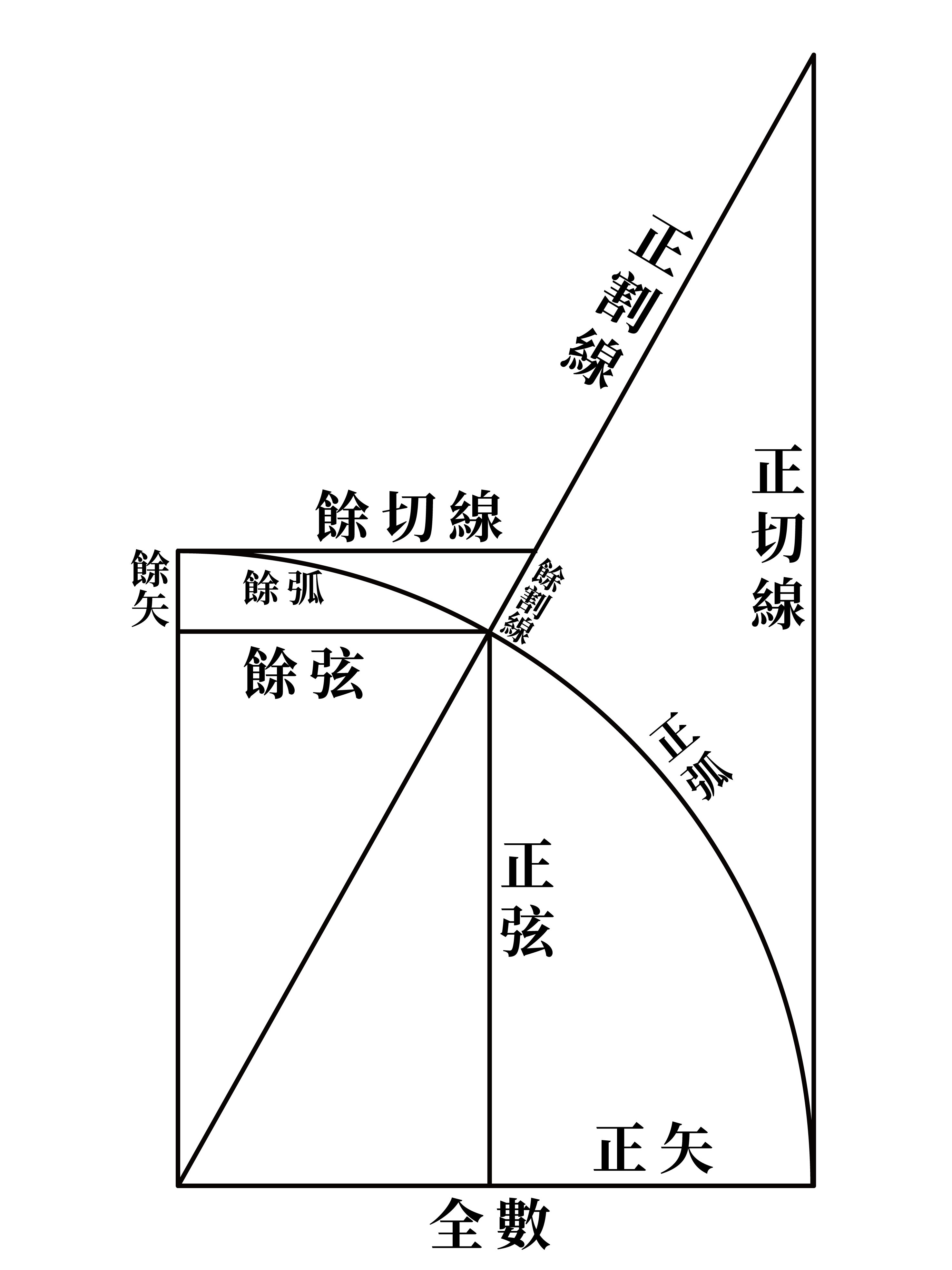數學英文

三角比

三角學 (trigonometry) 是從「三角」與「測量」兩個字根合併而成的， 可以理解它原本是以三角測量為主要目地的數學次領域 (a branch of mathematics)。 Trigonometry 的基本物件是直角三角形 (right triangles) 任取兩邊的比值所定義的 6 個三角比 (trigonometric ratios)： 正弦 sine (sin), 餘弦 cosine (cos), 正切 tangent (tan), 餘切 cotangent (cot), 正割 secant (sec), 和餘割 cosecant (csc)。 在 calculator 淘汰 (obsolete) 了三角表 (trigonometry tables) 之後， 常用的三角比剩下三個：sin, cos, and tan。 為了發展微積分公式，sec 還扮演重要的角色，但 cot 和 csc 可以完全被 tan 和 sin 的倒數取代而不至於造成不便。

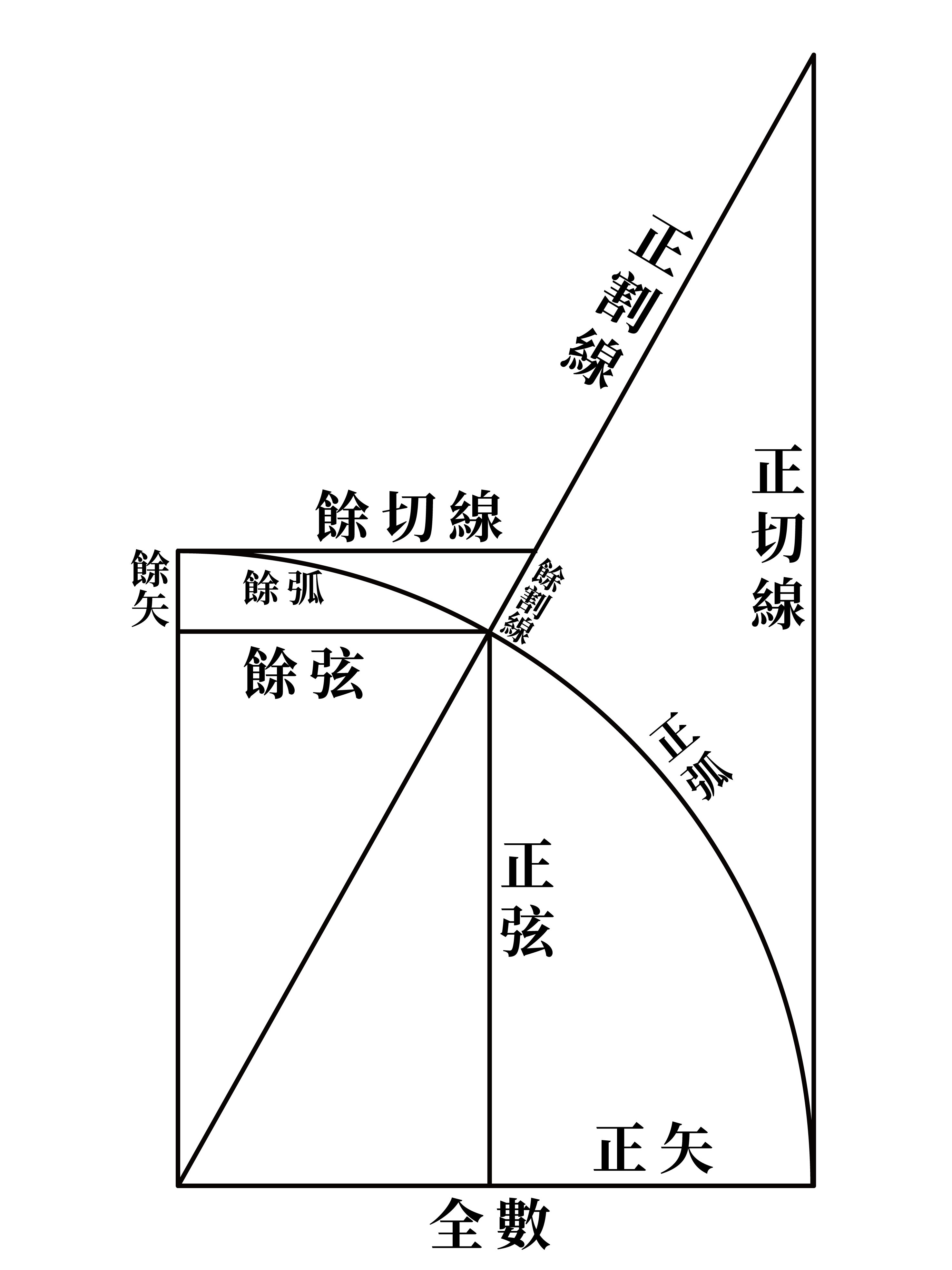三角比的名稱 tangent 和 secant 本來就是切線與割線的意思， sine 則是從印度的「半弦」經過阿拉伯文和拉丁文再成為英文的。 這些名稱的來源是因為它們原本是圓心角 (central angle) 所決定的某些線段長， 如下圖，可以看到切線、割線的出現。 在圓上討論各線段長，就獲得比 6 個更多的三角比， 例如正矢 (versine) 和餘矢 (coversine)。

當直角三角形的 two legs 擺成水平、鉛直 (horizontal / vertical) 形式時， 水平的邊稱為底 (base)，鉛直的邊稱為高 (perpendicular)。 當指定了直角三角形的一個銳角 A 時，垂直的兩邊，一個稱為角 A 的鄰邊 (adjacent side) 另一邊稱為對邊 (opposite side)。 以角 A 為「主角」時，直角三角形的另一個銳角就是它的餘角 (complementary angle)。 三個「餘」三角比英文名稱的 co- 都是 complementary 的縮寫， 指的是「餘角的比」，例如角 A 的餘弦 cosine of A 是餘角的正弦 sine of the complementary of A。 沒有標準的餘角符號，某些老師用 A^c 表示 A 的餘角。

像 \(30^\circ\)（30 度、30 degrees，\(\displaystyle{\pi\over6}\)）、 \(45^\circ\) （\(\displaystyle{\pi\over4}\)）、 \(60^\circ\) （\(\displaystyle{\pi\over3}\)） 這些常用來舉例的角， 稱為特殊角 (special angles) 或普通角 (common angles)。 事實上，特殊角還有 \(15^\circ\) （\(\displaystyle{\pi\over12}\)）、 \(18^\circ\) （\(\displaystyle{\pi\over10}\)）、 \(22.5^\circ\) （\(\displaystyle{\pi\over8}\)）、 \(36^\circ\) （\(\displaystyle{\pi\over5}\)），以及它們的餘角。

正切也跟斜率和坡度有關。 傾角 (angle of inclination 或 dip angle) 為 \(\alpha\) 的直線斜率 (slope) 是 \(\tan\alpha\)，而坡度 (grade) 其實就是斜率，只是習慣寫成百分比： \[\text{grade}\alpha = \tan\alpha\times 100\% = {\text{rise}\over\text{run}}\times 100\%\]