數學英文

三角形的測量

三角形面積 (area) 是同底同高長方形面積的一半，所以基本公式是

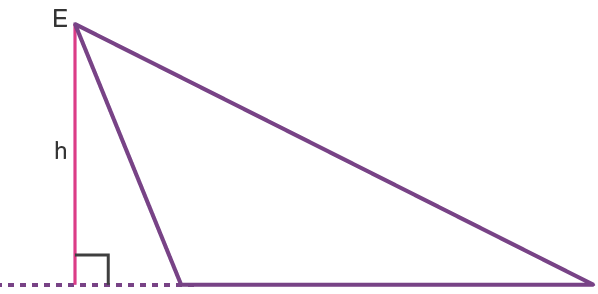三角形可取任一邊當底，所謂高 (height) 是從對角到底的距離 (distance)， 而所謂距離是從點到底邊延伸直線 (extended base) 的垂直線段的長度： length of the line segment through the opposite vertex and perpendicular to the extended base。 「高」可同時指那條垂直線段或者它的長度，而 height 的意思只是長度， 用 altitude 指那條垂直線段；但是 altitude 也可以指 height。 高與（延長）底的交點稱為高的垂足 (the foot of the altitude)， 從某頂點 \(B\) 作高是說 the altitude dropped from the vertex \(B\)， 在某邊 \(b\) 上作高是說 the altitude drawn to the side \(b\)。

既然三角形的全等條件 (Triangle Congruence Conditions) 可以決定唯一的三角形， 它們就應該能決定三角形的三邊長、三個角，與面積。簡述如下。

RHS（已知直角三角形的斜邊與一股）

用畢氏定理求另一股，用基本公式算面積，反查「正切表」(Tangent Table)， 亦即使用 arctan (arc-tangent) 得到兩個銳角的角度。

SAS（已知兩邊及其夾角）

這個條件就是面積的正弦公式： \[|\triangle ABC| = {1\over2}ab\sin C\] 其中絕對值符號 \(\triangle ABC\) 表示三角形 \(ABC\) 的面積。 用餘弦定理算出第三邊，用面積求另兩個角的正弦，再反查「正弦表」(Sine Table)， 亦即使用 arcsin (arc-sine) 得知角度。 如果遇到鈍角，則取 arcsin 之補角。

ASA 或 AAS（已知兩角及任一邊）

用內角和定理得知第三角，用正弦定理得知另兩邊，用正弦公式算面積。

SSS（已知三邊長）

用海龍公式算面積，從面積求各角的正弦，再用 arcsin 查角度。

三角形的三個高交於一點，那一點稱為三角形的垂心 (orthocenter)， 字首 ortho- 來自於 orthogonal 即垂直／正交之意。 垂心的應用很少，它或許屬於數學的「人文」內容。

另一類人文課題是三角形的旁心 (excenters)，共有三個， 它們是三個旁切圓 (excircles / escribed circles) 的圓心。 對應頂點 \(A\) 的旁心稱為 the excenter of \(A\)。