


Next: About this document ...
Up: 高中單變數微積分的補充
Previous: L'Hôpital's Rule
在本節中我們介紹定積分觀念的一項推廣─即引入瑕積分的概念.
在我們定義定積分時, 我們假定被積分函數有界,
又假定積分的間隔為一有限間隔. 為了取消這些限制,
Cauchy 引入了瑕積分的概念. 先讓我們看一個例子:
我們知道對任意實數 T,  都可以用積分
都可以用積分
表示.
大家通常又認為
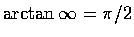 .
所以我們希望能把積分
.
所以我們希望能把積分
解釋為 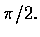
Cauchy 引入了瑕積分 (improper integral) 的觀念,
就是為了合理地解釋這類問題.
以下我們把以前所講過的積分稱為正常積分 (proper integral).
我們要定義的瑕積分呈
之形,
其中 a,b 代表實數或符號 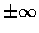 ,
而且函數 f(x) 不一定有界.
以下我們用 I 表示此瑕積分, 其定義要分以下數款說明:
,
而且函數 f(x) 不一定有界.
以下我們用 I 表示此瑕積分, 其定義要分以下數款說明:
(1)
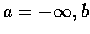 為實數, 且對任意
為實數, 且對任意
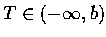 ,
積分
,
積分
均為正常積分. 如果極限
存在且為有限值, 此時我們把 I 定義為該極限.
((2)
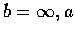 為實數, 且對任意
為實數, 且對任意
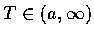 ,
積分
,
積分
均為正常積分. 如果極限
存在且為有限值, 此時我們把 I 定義為該極限.
(3) a,b 均為實數, a<b, 函數 f(x) 無界, 但對任意 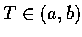 ,
積分
,
積分
均為正常積分.
如果當 T 從 a 的右側趨近於 a 時,
極限
存在且為有限值,
此時我們把 I 定義為該極限.
(4) a,b 均為實數, a<b, 函數 f(x) 無界, 但對任意
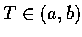 ,
積分
,
積分
均為正常積分.
如果當 T 從 b 的左側趨近於 b 時,
極限
存在且為有限值,
此時我們把 I 定義為該極限.
(5) 一般情形. 假定我們能選擇 n-1 個實數
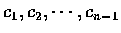 使
使
 ,
且使每個積分
,
且使每個積分
均為正常積分或為 (1)-(4) 中所定義的瑕積分. 此時我們把 I 定義為
注意在這個定義中, I 的值和 n 及分點
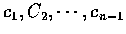 的選擇全都無關;
這就是說如果我們也能選擇 m-1 個實數
的選擇全都無關;
這就是說如果我們也能選擇 m-1 個實數
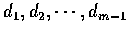 使
使
 ,
且使每個積分
,
且使每個積分
均或為正常積分或為 (1)-(4) 中所定義的瑕積分,
則必有
這結果讀者試自行證之.我們將結果的一部分留作習題.
(6) 若 b<a, 則定義
在以上 (1)-(6) 諸款中, 積分 I 有一個固定的有限值.
此時也可以說 Cauchy 的瑕積分 I 收斂(converge).
在 (1)-(4) 諸款中, 如果所談的極限不存在, 或 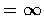 或
或 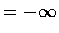 ,
我們便說 I 發散 (diverge). 在情形 (5) 中, 如果諸積分
,
我們便說 I 發散 (diverge). 在情形 (5) 中, 如果諸積分
中至少有一個發散, 我們便說 I 發散.
對瑕積分有了這些瞭解以後, 本節開始所舉的例子便可完全 justify 了:
現在讓我們再舉兩個有趣的例子: 設 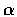 為正實數.
我們將考慮
為正實數.
我們將考慮
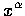 的積分:
的積分:
(I)
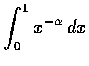 .
這積分當
.
這積分當 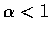 時收斂到
時收斂到
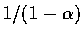 ,
當
,
當
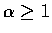 時發散.
時發散.
(II)
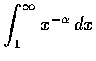 .
這積分當
.
這積分當 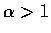 時收斂到
時收斂到
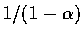 ,
當
,
當
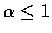 時發散.
時發散.
有時我們也把面積和體積的觀念應用到無界的區域去.
例 4
求曲線
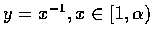
與
x軸所夾的面積和這面積圍繞
x 軸旋轉所得的體積.
解. 所求的面積應為
但這積分發散, 故面積無限. 又所求的體積為
這卻是有限的體積了.
習

題
- 1.
- 決定下列各積分何者收斂, 何者發散, 並求出收斂者的值:
(a)
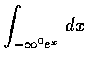 ,
(b)
,
(b)
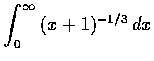 ,
(c)
,
(c)
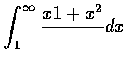 (d)
(d)
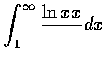 ,
(e)
,
(e)
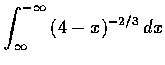 ,
(f)
,
(f)
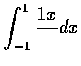
- 2.
- 設
問
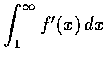 為收斂或發散?
若收斂, 則求其值.
為收斂或發散?
若收斂, 則求其值.
- 3.
- Evaluate
- 4.
- 設 f(x) 為定義在
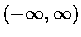 上的函數, a,b 為實數. 假定
上的函數, a,b 為實數. 假定
試證
- 5.
- (a) 試證若
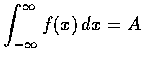 ,
則
,
則
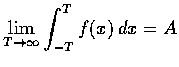 .(b) 試求一函數 f(x),
使
.(b) 試求一函數 f(x),
使
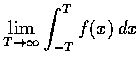 得有限值,
但
得有限值,
但
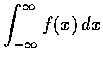 發散.
發散.



Next: About this document ...
Up: 高中單變數微積分的補充
Previous: L'Hôpital's Rule
1999-06-27
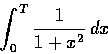
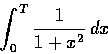
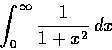
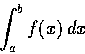
![]() 為實數, 且對任意
為實數, 且對任意
![]() ,
積分
,
積分
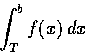
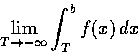
![]() 為實數, 且對任意
為實數, 且對任意
![]() ,
積分
,
積分
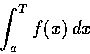
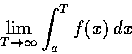
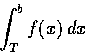
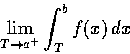
![]() ,
積分
,
積分
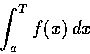
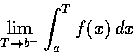
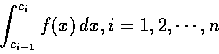
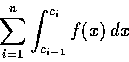
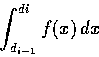
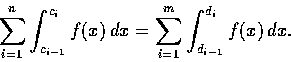
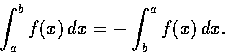
![]() 或
或 ![]() ,
我們便說 I 發散 (diverge). 在情形 (5) 中, 如果諸積分
,
我們便說 I 發散 (diverge). 在情形 (5) 中, 如果諸積分
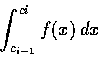
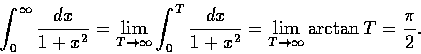
![]() 為正實數.
我們將考慮
為正實數.
我們將考慮
![]() 的積分:
的積分:
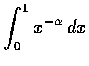 .
這積分當
.
這積分當 ![]() 時收斂到
時收斂到
![]() ,
當
,
當
![]() 時發散.
時發散.
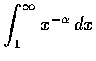 .
這積分當
.
這積分當 ![]() 時收斂到
時收斂到
![]() ,
當
,
當
![]() 時發散.
時發散.
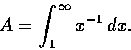
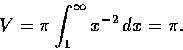
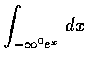 ,
(b)
,
(b)
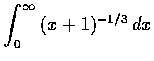 ,
(c)
,
(c)
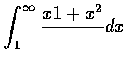 (d)
(d)
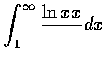 ,
(e)
,
(e)
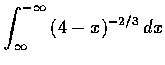 ,
(f)
,
(f)
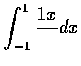
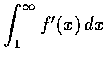 為收斂或發散?
若收斂, 則求其值.
為收斂或發散?
若收斂, 則求其值.
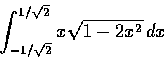
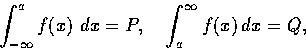
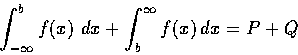
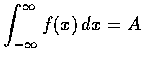 ,
則
,
則
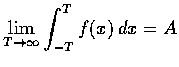 .(b) 試求一函數 f(x),
使
.(b) 試求一函數 f(x),
使
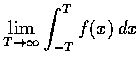 得有限值,
但
得有限值,
但
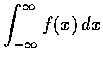 發散.
發散.