


Next: Higher Order Derivatives
Up: 多變數函數的微分學
Previous: Chain Rule and the
再假定 G 上過 (p, f(p)) 點的可微曲線 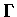 的方程式為
的方程式為
並假定
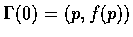 .
則因
.
則因
由 chian rule 得
亦即
所以 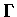 曲線在 (p,f(p)) 處的切線和
曲線在 (p,f(p)) 處的切線和
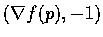 垂直.
垂直.
反之, 設 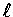 為過 (p,f(p)) 且和
為過 (p,f(p)) 且和
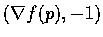 垂直的直線.
可設
垂直的直線.
可設 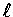 的方程式為
的方程式為
式中
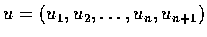 符合
符合
令
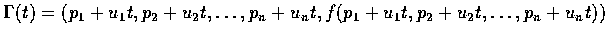 ,
,
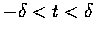 則
則 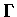 在 G 上,
在 G 上, 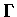 可微,
可微,
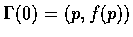 ,
且
,
且
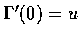 .
所以有如下之結論: 在 f 的函數圖上過 (p,f(p))點的所有可微曲線在這點處的切線剛好構成過
(p,f(p)) 點以
.
所以有如下之結論: 在 f 的函數圖上過 (p,f(p))點的所有可微曲線在這點處的切線剛好構成過
(p,f(p)) 點以
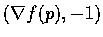 為法向量的超平面.
很自然地, 我們稱此超平面 G 在 (p,f(p)) 處的切空間 (tangent space)
或切超平面 (tangent hyperplane).
在
為法向量的超平面.
很自然地, 我們稱此超平面 G 在 (p,f(p)) 處的切空間 (tangent space)
或切超平面 (tangent hyperplane).
在
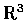 中曲面的切空間叫切平間 (tangent plane).
令
中曲面的切空間叫切平間 (tangent plane).
令
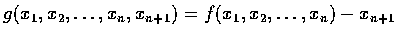 ,
,
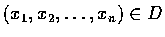 ,
,
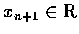 .
則 G 可視為方程式
.
則 G 可視為方程式
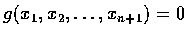 的圖形.
令
P = (p,f(p)).
則
的圖形.
令
P = (p,f(p)).
則
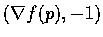 就是
就是
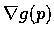 .
上面的結果可以說成:
.
上面的結果可以說成:
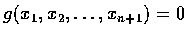 在 P 處的切空間即過 P 點以
在 P 處的切空間即過 P 點以
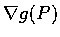 為法向量的超平面.
為法向量的超平面.
一般而言, 考慮方程式
假定可將xn+1從此式解出; 換言之, 即假定上文所討論的區域 D 上的函數圖
xn+1 = f(x) 所表示的超曲面 S 滿足這個方程式:
再假定
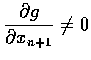 .
將此式關於xk微分, 其中
.
將此式關於xk微分, 其中
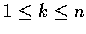 ,
則有
,
則有
從而乃得
令
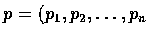 ,
pn+1 = f(p),
,
pn+1 = f(p),
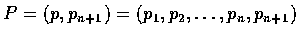 .
則
.
則 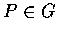 ,
g(P) = 0, 且
,
g(P) = 0, 且
故知所求的切超平面此時可以寫成下形:
因為 xn+1在此式中沒有特殊的地位,
所以從方程式 g(X) = 0將
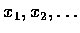 ,
或 xn 解出,
都會得到同一個切超平面的方程式.
,
或 xn 解出,
都會得到同一個切超平面的方程式.
例 8
Find the tangent plane to the quadric surface
a1x21+a2x22+a3x23+b1x2x3+b2x3x1+b3x1x2+c1x1+c2x2+c3x3+d=0
at the point
p= (
p1,
p2,
p3 ) on the surface.
Solution. Let us denote the lift-hand side of the equation of the surface by
g(x1,x2,x3). Then
Since p lies on the quadric surface, we have
-a1p21-a2p22-a3p23-b1p2p3-b2p3p1-b3p1p2 = d+c1p1+c2p2+c3p3.
Hence
Therefore the equation of the tangent plane is
回到函數 f 的情形. f 的函數圖 G 在 (p, f(p)) 處切空間 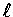 的方程式為
的方程式為
即
此切空間亦可視為
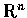 上函數
上函數
的圖形. L(x)和f(x)在 p 點附近有密切的關係, 此即下述定理的內容:
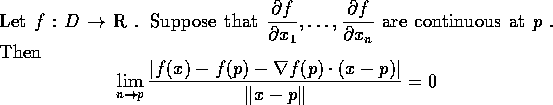
證明. 當 x 和 p 充分接近時有
式中
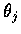 由 x 決定, 且
由 x 決定, 且
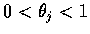 .
故得
.
故得
因
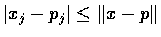 , 所以若
, 所以若 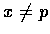 則
則
從
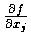 在 p 點的連續性知右邊當
在 p 點的連續性知右邊當
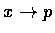 時趨於 0. 明所欲證.
時趨於 0. 明所欲證.
Definition. The function df
of variables (p,v) defined by
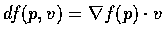 is called the differential (微分)
of f at p with increment v. The differential is also
known as the total differential (全微分)
or the exact differential (正合微分).
is called the differential (微分)
of f at p with increment v. The differential is also
known as the total differential (全微分)
or the exact differential (正合微分).
上定理便是說: 當 x 和 p 接近時,
f(x) - f(p) 可以用 d f 代替,
而誤差可以容忍.



Next: Higher Order Derivatives
Up: 多變數函數的微分學
Previous: Chain Rule and the
1999-06-28
![]() 為過 (p,f(p)) 且和
為過 (p,f(p)) 且和
![]() 垂直的直線.
可設
垂直的直線.
可設 ![]() 的方程式為
的方程式為
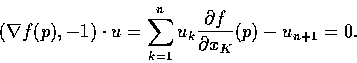
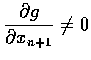 .
將此式關於xk微分, 其中
.
將此式關於xk微分, 其中
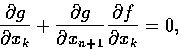
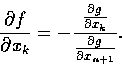
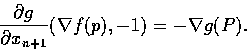
![\begin{eqnarray*}\lefteqn{\nabla g(p) \cdot (x - p)}\\
&=& 2a_{1}p_{1}x_{1}+b_{...
...}}{2}+c_{2}\frac{x_{2}+p_{2}}{2}+c_{3}\frac{x_{3}+p_{3}}{2}+d].
\end{eqnarray*}](img154.gif)
![]() 的方程式為
的方程式為
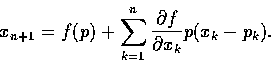
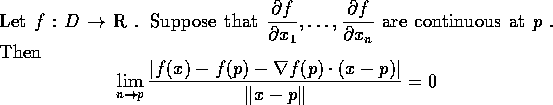
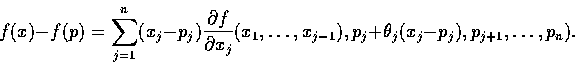
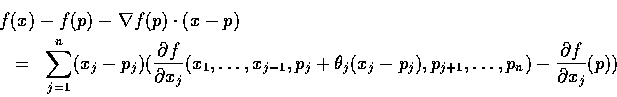
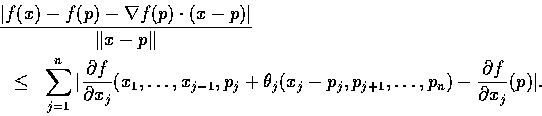
![]() is called the differential (微分)
of f at p with increment v. The differential is also
known as the total differential (全微分)
or the exact differential (正合微分).
is called the differential (微分)
of f at p with increment v. The differential is also
known as the total differential (全微分)
or the exact differential (正合微分).