定理 1.
設 Q 是一實係數多項式, 則 Q 可分解成一些實係數的一次式及不可約二次式的乘積.
定理 2.
設
R(x)=P(x)/Q(x) 是一實係數的真有理式. 設 Q 分解成
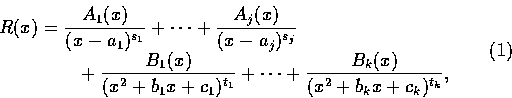
定理 3.
設
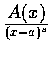 是一實係數真有理式,
則必有實數
是一實係數真有理式,
則必有實數
![]() 使得
使得
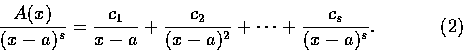
定理 4.
設
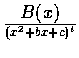 是一實係數真有理式,
則必有實數
是一實係數真有理式,
則必有實數
![]() 使得
使得
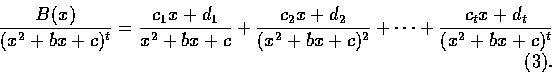
假若對 (1) 式右邊每項分別引用定理 3 或定理 4, 則 P(x)/Q(x) 分解成一些如 (2)、(3) 式中右邊型態的分式的和, 這過程通常稱為把 P(x)/Q(x) 化成部分分式 (partial fractions).
如何將有理函數實際地化成部分分式? 我們在後面的例子裡示範一些技巧.