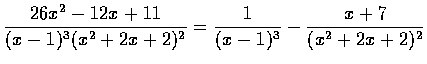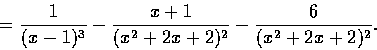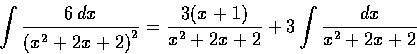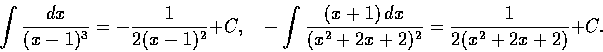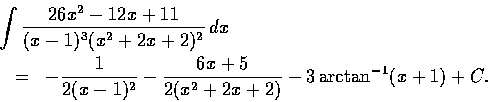Next: 三角函數的有理式的積分
Up: 部分分式
Previous: 部分分式的理論基礎
設 P(x) 和 Q(x) 為二具實係數的多項式,
R(x)=P(x)/Q(x).
利用長除法可把 R(x) 寫成一多項式及一真有理函數的和.
多項式的積分以前說明過了. 真有理式化成部分分式後, 其積分不出下列四種型態.
證明. 令
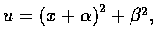 則
則
下面舉例說明如何把真有理式化為部分分式的和,
再把這些部分分式轉換成上面四個型態來積分.
例 20
求
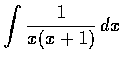
.
解. 我們用未定係數法求分項分式. 從定理知可設
注意此式只當
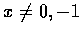 時始有意義. 此時有
時始有意義. 此時有
令
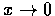 ,
得 A=1. 又令
,
得 A=1. 又令
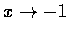 ,
得 B=-1. 故
,
得 B=-1. 故
注意在本例中我們說令
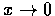 及令
及令
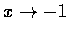 ,
而不說令 x=0 及令 x=-1. 這是由於分式
,
而不說令 x=0 及令 x=-1. 這是由於分式
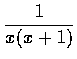 的定義域不包含 0, 也不包含 -1 的緣故.
的定義域不包含 0, 也不包含 -1 的緣故.
一般地講, 用未定係數法決定係數, 除上述的方法外, 還有另一方法;
即當兩個多項式的值在無限多個點處相等, 則二多項式恆等,
所以其對應同冪項的係數皆相等. 下例說明這方法:
例 21
求
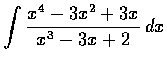
.
解.
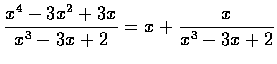 .
因
.
因
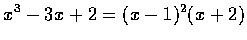 ,
故可設
,
故可設
即
此式為恆等式, 因為已知兩邊在 x=1 及 x=-2 以外的點處都相等.
比較同冪項的係數乃得
解之, 得
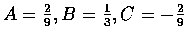 .
故
.
故
例 22
求
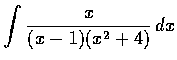
.
解. 設
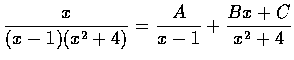 解之, 得
解之, 得
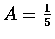 ,
,
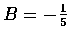 ,
,
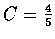 .
而
.
而
故
例 23
求
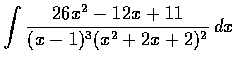
.
解. 計算後可得
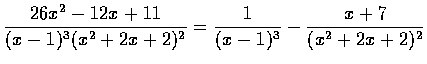
由以上型 4 得
而
故



Next: 三角函數的有理式的積分
Up: 部分分式
Previous: 部分分式的理論基礎
1999-06-27
![\begin{displaymath}\begin{array}{ll}
1.&\displaystyle\int \frac{a\,dx}{(ax+b)^{n...
...{dx}{[(x+{\alpha})^2+{\beta}^2]^{n-1}}.
\end{array}\end{array}\end{displaymath}](img99.gif)
![\begin{displaymath}\begin{array}{ll}
1.&\displaystyle\int \frac{a\,dx}{(ax+b)^{n...
...{dx}{[(x+{\alpha})^2+{\beta}^2]^{n-1}}.
\end{array}\end{array}\end{displaymath}](img99.gif)
![]() 則
則
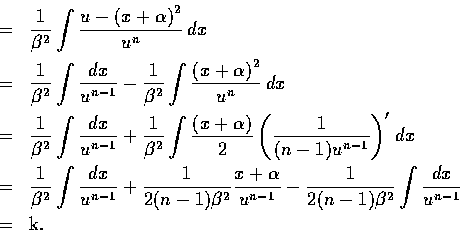
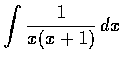 .
.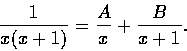
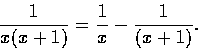
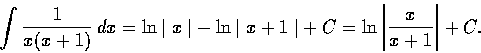
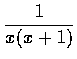 的定義域不包含 0, 也不包含 -1 的緣故.
的定義域不包含 0, 也不包含 -1 的緣故.
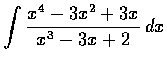 .
.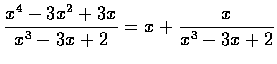 .
因
.
因
![]() ,
故可設
,
故可設
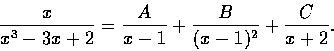
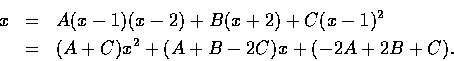
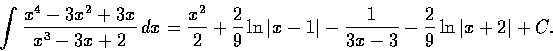
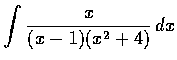 .
.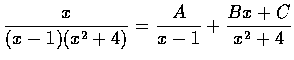 解之, 得
解之, 得
![]() ,
,
![]() ,
,
![]() .
而
.
而
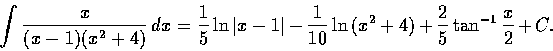
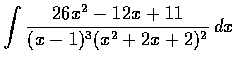 .
.