Chain Rule and the Gradient

First we extend the chain rule to functions of several variables.

Proof. Let $\gamma_{k} (t)$ be the components of $\gamma (t)$, i.e.,

$$\gamma (t) = (\gamma_{1} (t), \gamma_{2} (t),\ldots , \gamma_{n} (t)).$$

We define the vector-valued function $\overline{x}_{0} (t),\ldots , \overline{x}_{n} (t)$ by putting

$$\overline{x}_{j} (t) = (\gamma_{1} (t),\ldots , \gamma_{j} (t), \gamma_{j+1} (0),\ldots , \gamma_{n} (0)).$$

Then

$$f(\gamma (t)) - f(\gamma (0)) = \sum_{j=1}^{n} [f(\overline{x}_{j} (t)) - f(\overline{x}_{j-1} (t))].$$

Applying the mean-value theorem, we have for $\mid t \mid$ sufficiently small,

$$\begin{eqnarray*}\lefteqn{f(\bar{x}_{j}(t)) - f(\bar{x}_{j - 1}(t))}\\ &=& (r_{... ...ots, r_{j - 1}(t), \varphi_{j} (t), p_{j + 1}, \ldots , p_{n}). \end{eqnarray*}$$

where $\varphi_{j} (t)$ lies between p_j and r_j(t). Since

$$\lim_{t \rightarrow {0} } \frac{r_{j} (t) - r_{j} (0)}{t} = u_{j}$$

and

$$\lim_{t \rightarrow {0} } \frac{\partial f}{\partial x_{j} } ... ... \frac{\partial f}{\partial x_{j} } (p_{1} ,\cdots , p_{n} ),$$

we have

$$\left. \frac{d}{dt} f(r(t)) \right\vert _{t=0} = \lim_{t \rig... ...(0))}{t} = \sum u_{j} \frac{\partial f}{\partial x_{j} } (p).$$

Q. E. D.

Corollary Let $D \subse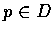t \mathbb{R} ^{n}$, $f : D \longrightarrow \mathbb{R}$and $p \in D$. Suppose that $$\frac{\partial f}{\partial x_{1} } ,\cdots , \frac{\partial f}{\partial x_{n} }$$are all defined in a neighborhood of p and are continuous at p. Then for every vector $u =(u_{1} ,\ldots , u_{n} )$, the derivative D_u f(p) exists and is given by

$$D_{u} f(p) = \sum_{j=1}^{n} u_{j} \frac{\partial f}{\partial x_{j} } (p) .$$

例 7   Let $f(x,y,z) = x^{2} y + y^{2} z , g(u,v) = u + v , \, h(u,v) = u - v , j(u) = e^{u}$ ,

F(u,v) = f(g(u,v), h(u,v), j(u)).

Compute F_u and F_v.

Solution. To compute F_u, we treat v as a constant and apply the chain rule. Thus we have

$$\begin{eqnarray*}F_{u}(u,v) & = & f_{x}g_{u} + f_{y}h_{u} + f_{z}j'(u) \\ & = &... ...}e^{u} \\ & = &3u^{2} + 2uv - v^{2} + (u - v)(2 + u - v)e^{u}. \end{eqnarray*}$$

Similarly,

$$\begin{eqnarray*}F_{v}(u,v) & = & f_{x}g_{v} + f_{y}h_{v} \\ & = & 2xy - x^{2} ... ...- 2(u + v)e^{u} \\ & = & u^{2} - 2uv - 3v^{2} - 2(u - v)e^{u}. \end{eqnarray*}$$

Set

$$\nabla f(p) = (\frac{\partial f}{\partial x_{1} } (p),\ldots , \frac{\partial f}{\partial x_{n} } (p)).$$

This vector in 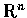$\mathbb{R} ^{n}$ is called the gradient (梯度) of f at p. It is also written as grad f. The symbol $\nabla$ is pronounced nabla or atled. Under the conditions of Corollarry, we have

$$D_{u} f(p) = \nabla f(p)\, \cdot \, u$$

for all $u \in \mathbb{R} ^{n}$.

設 $\nabla f(P) \neq {0}$. 令 $r = \parallel \nabla f(p) \parallel, v = \nabla f(p)/r$. 則 v 為單位向量. 由 Cauchy 不等式知對任意單位向量 u 有

$$D_{u} f(p) = \nabla f(p)\cdot u = rv \cdot u \leq r \parallel u \parallel \, \parallel v \parallel =r .$$

等式成立的充要條件是 $u\cdot v=\parallel u \parallel \, \parallel v \parallel =1$, 即 u=v. 因此有

換言之, 梯度的方向就是 f 增加最快的方向, 其大小乃是這個最快的增加率. $-\nabla f(p)$ 的方向也就是 f 減少最快的方向, 其大小當然也是這個最快的減少率.