Tangent Spaces and Differentials

再假定 G 上過 (p, f(p)) 點的可微曲線 $\Gamma$ 的方程式為

$$\Gamma(t) = (x_{1} (t),x_{2} (t),\ldots,x_{n} (t),x_{n+1} (t)), \quad -\delta < t < \delta ,$$

並假定 $\Gamma(0) = (p,f(p))$. 則因

$$x_{n + 1} (t) = f(x_{1} (t),x_{2} (t),\ldots,x_{n} (t)),$$

由 chian rule 得

$$x'_{n+1} (0) = \nabla f(p) \cdot (x'_{1} (0),x'_{2} (0),\ldots,x'_{n} (0)).$$

亦即

$$(\nabla f(p),-1) \cdot \Gamma'(0) = 0$$

所以 $\Gamma$ 曲線在 (p,f(p)) 處的切線和 $(\nabla f(p),-1)$ 垂直.

反之, 設 $\ell$ 為過 (p,f(p)) 且和 $(\nabla f(p),-1)$ 垂直的直線. 可設 $\ell$ 的方程式為

$$\ell(t) = (p,f(p)) + tu, \quad t \in \mathbb{R}$$

式中 $u = (u_{1},u_{2},\ldots , u_{n} , u_{n+1} )$ 符合

$$(\nabla f(p),-1) \cdot u = \sum_{k=1}^{n} u_{k} \frac {\partial f}{\partial x_{K} }(p) - u_{n+1} = 0.$$

令 $\Gamma(t) = (p_{1}+u_{1}t,p_{2}+u_{2}t,\ldots ,p_{n}+u_{n}t, f(p_{1}+u_{1}t,p_{2}+u_{2}t,\ldots ,p_{n} +u_{n} t))$, $-\delta < t < \delta$ 則 $\Gamma$ 在 G 上, $\Gamma$ 可微, $\Gamma(0) = (p,f(p))$, 且 $\Gamma'(0) = u$. 所以有如下之結論: 在 f 的函數圖上過 (p,f(p))點的所有可微曲線在這點處的切線剛好構成過 (p,f(p)) 點以 $(\nabla f(p),-1)$ 為法向量的超平面. 很自然地, 我們稱此超平面 G 在 (p,f(p)) 處的切空間 (tangent space) 或切超平面 (tangent hyperplane). 在 $\mathbb{R} ^3$ 中曲面的切空間叫切平間 (tangent plane). 令 $g(x_{1},x_{2},\ldots,x_{n},x_{n+1} )=f(x_{1},x_{2},\ldots,x_{n} )-x_{n+1}$, $(x_{1},x_{2},\ldots , x_{n} ) \in D$, $x_{n+1} \in \mathbb{R}$. 則 G 可視為方程式 $g(x_{1} , x_{2} , \ldots , x_{n+1} )=0$ 的圖形. 令 P = (p,f(p)). 則 $(\nabla f(p),-1)$ 就是 $\nabla g(p)$. 上面的結果可以說成: $g(x_{1} , x_{2} , \ldots , x_{n+1} )=0$ 在 P 處的切空間即過 P 點以 $\nabla g(P)$為法向量的超平面.

一般而言, 考慮方程式

$$g(X) = 0, \hbox to 1.5true cm{\hfill} X = (x,x_{n+1}), \, \, x = (x_{1},x_{2}, \ldots,x_{n} ).$$

假定可將x_n+1從此式解出; 換言之, 即假定上文所討論的區域 D 上的函數圖 x_n+1 = f(x) 所表示的超曲面 S 滿足這個方程式:

$$g(x_{1},\ldots ,x_{n}, f(x_{1},\ldots ,x_{n} )) = 0.$$

再假定 $$\frac{\partial g}{\partial x_{n+1}} \neq 0$$. 將此式關於x_k微分, 其中 $1 \leq k \leq n$, 則有

$$\frac{\partial g}{\partial x_{k} } + \frac{\partial g}{\partial x_{n+1} } \frac {\partial f}{\partial x_{k} } = 0,$$

從而乃得

$$\frac{\partial f}{\partial x_{k} } = -\frac {\frac {\partial g}{\partial x_{k} } } {\frac {\partial g}{\partial x_{n+1} } } .$$

令 $p = (p_{1},p_{2},\ldots ,p_{n}$, p_n+1 = f(p), $P = (p,p_{n+1}) = (p_{1},p_{2} ,\ldots ,p_{n},p_{n+1})$. 則 $P \in G$, g(P) = 0, 且

$$\frac{\partial g}{\partial x_{n+1} } (\nabla f(p),-1) = -\nabla g(P).$$

故知所求的切超平面此時可以寫成下形:

$$\nabla g(P) \cdot (X-P) = 0.$$

因為 x_n+1在此式中沒有特殊的地位, 所以從方程式 g(X) = 0將 $x_{1}, x_{2}, \ldots$, 或 x_n 解出, 都會得到同一個切超平面的方程式.

例 8   Find the tangent plane to the quadric surface

a₁x²₁+a₂x²₂+a₃x²₃+b₁x₂x₃+b₂x₃x₁+b₃x₁x₂+c₁x₁+c₂x₂+c₃x₃+d=0

at the point p= (p₁,p₂,p₃ ) on the surface.

Solution. Let us denote the lift-hand side of the equation of the surface by g(x₁,x₂,x₃). Then

$$\nabla g(p) = (2a_{1}p_{1}+b_{2}p_{3}+b_{3}p_{2}+c_{1}, 2a_{2... ...+b_{1}p_{3}+c_{2}, 2a_{3}p_{3}+b_{1}p_{2}+b_{2}p_{1}+c_{3}. )$$

Since p lies on the quadric surface, we have

-a₁p²₁-a₂p²₂-a₃p²₃-b₁p₂p₃-b₂p₃p₁-b₃p₁p₂ = d+c₁p₁+c₂p₂+c₃p₃.

Hence

$$\begin{eqnarray*}\lefteqn{\nabla g(p) \cdot (x - p)}\\ &=& 2a_{1}p_{1}x_{1}+b_{... ...}}{2}+c_{2}\frac{x_{2}+p_{2}}{2}+c_{3}\frac{x_{3}+p_{3}}{2}+d]. \end{eqnarray*}$$

Therefore the equation of the tangent plane is

$$a_{1}p_{1}x_{1}+a_{2}p_{2}x_{2}+a_{3}p_{3}x_{3}+b_{1}\frac{p_{2}x_{3}+p_{3}x_{2}}{2}+b_{2}\frac{p_{3}x_{1}+p_{1}x_{3}}{2}$$

$$+b_{3}\frac{p_{1}x_{2}+p_{2}x_{3}}{2}+c_{1}\frac{x_{1}+p_{1}}{2}+c_{2}\frac{x_{2}+p_{2}}{2}+c_{3}\frac{x_{3}+p_{3}}{2}+d = 0.$$

回到函數 f 的情形. f 的函數圖 G 在 (p, f(p)) 處切空間 $\ell$的方程式為

$$( \frac{\partial f}{\partial x_{1}}(p) , \frac{\partial f}{\p... ..., x_{2} - p_{2}, . . . , x_{n} - p_{n}, x_{n+1} - f(p) ) = 0,$$

即

$$x_{n+1} = f(p) + \sum_{k=1}^{n}\frac{\partial f}{\partial x_{k}} p (x_{k} - p_{k}).$$

此切空間亦可視為 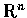$\mathbb{R} ^{n}$ 上函數

$$L(x) = f(p) + \nabla f(p) \cdot ( x - p )$$

的圖形. L(x)和f(x)在 p 點附近有密切的關係, 此即下述定理的內容:

證明. 當 x 和 p 充分接近時有

$$f(x) - f(p) = \sum_{j=1}^{n} (x_{j} - p_{j} ) \frac{\partial ... ...p_{j} + \theta_{j}(x_{j} - p_{j} ), p_{j+1} ,\ldots ,p_{n} ).$$

式中 $\theta_{j}$ 由 x 決定, 且 $0< \theta_{j} < 1$. 故得

$$\begin{eqnarray*}\lefteqn{f(x) - f(p) - \nabla f(p) \cdot (x - p)}\\ &=& \sum_{... ...p_{j+1} ,\ldots ,p_{n} )-\frac{\partial f}{\partial x_{j} } (p)) \end{eqnarray*}$$

因 $\vert x_{j} - p_{j} \vert \leq \Vert x - p \Vert$ , 所以若 $x \neq p$ 則

$$\begin{eqnarray*}\lefteqn{\frac{\vert f(x) - f(p) - \nabla f(p) \cdot (x - p)\ve... ...{j+1},\ldots ,p_{n})-\frac{\partial f}{\partial x_{j}}(p)\vert. \end{eqnarray*}$$

從 $\frac{\partial f}{\partial x_{j} }$ 在 p 點的連續性知右邊當 $x \rightarrow p$ 時趨於 0. 明所欲證.

Definition. The function df of variables (p,v) defined by $df(p,v) = \nabla f(p) \cdot v$ is called the differential (微分) of f at p with increment v. The differential is also known as the total differential (全微分) or the exact differential (正合微分).

上定理便是說: 當 x 和 p 接近時, f(x) - f(p) 可以用 d f 代替, 而誤差可以容忍.