Next: 極大和極小
Up: 多變數函數的微分學
Previous: Tangent Spaces and Differentials
If
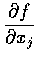 is difinied, it is
also a real valued function of n variables. The partial
derivatives of
is difinied, it is
also a real valued function of n variables. The partial
derivatives of
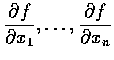 are called second order partial derivatives (二階偏導函數) of f.
It is customary to write
are called second order partial derivatives (二階偏導函數) of f.
It is customary to write
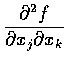 or
or
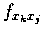 for
for
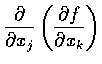 .
Derivatives of orders higher than 2 are definied similarly. Thus,
.
Derivatives of orders higher than 2 are definied similarly. Thus,
both denote the m th order partial derivative
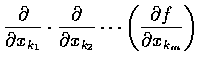 .
.
我們舉兩個簡單的例子如下:
例 9
令
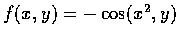
.
則
於是
例 10
令
f(x, y, z)=x3y2z. 則
fxy=fyx=6xyz,
且 fxyz, fxzy, fyzx, fyxz,
fzxy, fzyx 均等於 6x2y.
在這兩個例子裡都有
fxy=fyx,
而且關於不同變數的混合偏微分均似與變數的次序無關.
這項觀察大體不錯, 因為我們有下定理:
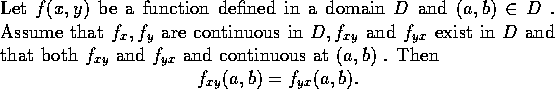
證明. 選擇 (x,y) 使 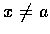 ,
,
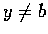 .
令
.
令
Q=f(x,y)-f(a,y)-f(x,b)+f(a,b)
先暫時固定 x, 定義
g(y)=f(x,y)-f(a,y). 則由均值定理得
式中 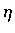 之值在 y 和 b 之間.
現在把 x 當成變數, 再用一次均值定理, 乃得
之值在 y 和 b 之間.
現在把 x 當成變數, 再用一次均值定理, 乃得
式中 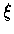 之值在 x 和 a 之間.
之值在 x 和 a 之間.
仿此先固定 y, 定義
h(x)=f(x, y)-f(x, b). 引用均值定理兩次乃得
式中 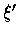 和
和 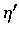 之值分別在 x, a 和 y, b 之間.
比較兩個 Q 式, 遂有
之值分別在 x, a 和 y, b 之間.
比較兩個 Q 式, 遂有
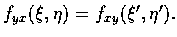 令
令
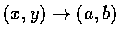 ,
由 fxy 和 fyx 的連續性知
,
由 fxy 和 fyx 的連續性知
明所欲證.
從以上的討論我們大體上可以相信
fyx=fxy 一般都成立了.
但事實上也有二者不相等的例子:
例 11
令
易證
f 在整個平面上連續. 若
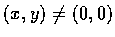
則
從而知
fx 在整個平面上連續. 因
f(
y,
x)=-
f(
x,
y), 故有
fx 也在整個平面上連續. 由以上的結果很容易算出
習

題
- 1.
- Show that the minimal distance from a point
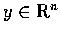 to the hyperplane through a point p with an unit normal
vector u is given by
to the hyperplane through a point p with an unit normal
vector u is given by
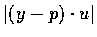 .
.
- 2.
- A curve which satisfies an equation of the form
Ax2+Bxy+Cy2+Dx+Ey+F=0.
is called a conic. Assume that this conic passes through the point (a,b).
Show that the tangent line to this conic at (a,b) is given by
- 3.
- Let
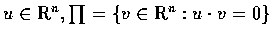 .
If
.
If
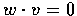 for all
for all
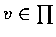 ,
show that
,
show that
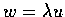 for some
for some
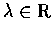 .
.
- 4.
- Show that every tangent plane to cone
z2=x2+y2.
intersects the cone in a straight line.
- 5.
- 試計算下列三函數的各二階偏導函數:(a)
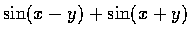 ,
(b)
,
(b)
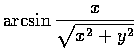 ,
(c)
,
(c)
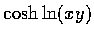 .
.
- 6.
- Let
u=x2siny+y2sinx.
Find
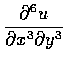 .
.
- 7.
- 設
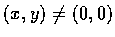 .
令
.
令
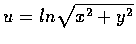 .
試證
.
試證
- 8.
- 設
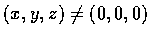 .
令
.
令
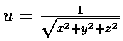 .
試證
.
試證
- 9.
- 定義函數
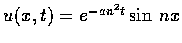 ,
式中 a 和 n 為常數. 試證明 u 滿足微分方程式
ut=auxx.
,
式中 a 和 n 為常數. 試證明 u 滿足微分方程式
ut=auxx.
- 10.
- (a) Let
F(t)=f(x,y) where
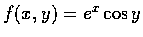 ,
x=t2, y=1-t3.
Compute F'(t) and F''(t) first by substitution and then by
the chain rule.
,
x=t2, y=1-t3.
Compute F'(t) and F''(t) first by substitution and then by
the chain rule.
(b) Do the same thing with
f(x,y,z)=ex2+y2+z2, 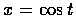 ,
,
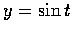 ,
z=t.
,
z=t.
- 11.
- 若
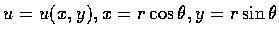 ,
試證明
,
試證明
- 12.
- 若
u=u(x, y, z),
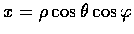 ,
,
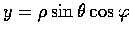 ,
,
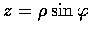 ,
試將
uxx+ uyy+uzz 用關於
,
試將
uxx+ uyy+uzz 用關於 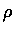 ,
,
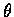 和
和 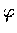 的偏導函數表出.
的偏導函數表出.



Next: 極大和極小
Up: 多變數函數的微分學
Previous: Tangent Spaces and Differentials
1999-06-28
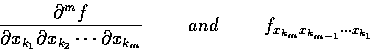
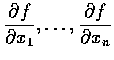 are called second order partial derivatives (二階偏導函數) of f.
It is customary to write
are called second order partial derivatives (二階偏導函數) of f.
It is customary to write
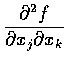 or
or
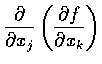 .
Derivatives of orders higher than 2 are definied similarly. Thus,
.
Derivatives of orders higher than 2 are definied similarly. Thus,
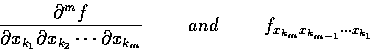
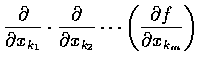 .
.
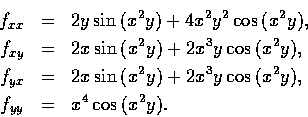
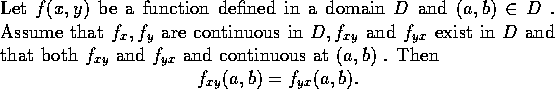
![]() ,
,
![]() .
令
.
令
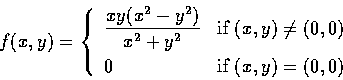
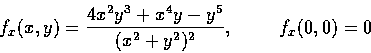
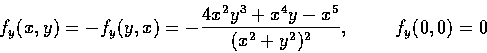
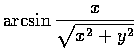 ,
(c)
,
(c)
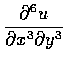 .
.