


Next: 二變數函數的重積分
Up: 線積分與重積分
Previous: 線積分與重積分
在本章和下章中, 我們將討論多變函數的積分學.
多變數函數的積分有很多種. 本章先討論線積分與重積分,
而把面積分和三重積分留給下章.
令
 ,
,
![$t \in [a, b]$](img2.gif) 為
為
 中的連續曲線,
若有
中的連續曲線,
若有
 使
使  局限在每個 [
ti-1, ti]
中時均有連續的導函數, (但當我們把
局限在每個 [
ti-1, ti]
中時均有連續的導函數, (但當我們把  看成整個
[a, b] 上的函數時, 不要求
看成整個
[a, b] 上的函數時, 不要求
 ,
存在), 則稱 C 為
,
存在), 則稱 C 為
 中的一條
piecewise continuously differentiable curve 或
piecewise smooth curve.
直觀地講,
piecewise smooth curve 是說這曲線除了在有限個點處可能轉硬灣外,
別的地方都到處平滑.
中的一條
piecewise continuously differentiable curve 或
piecewise smooth curve.
直觀地講,
piecewise smooth curve 是說這曲線除了在有限個點處可能轉硬灣外,
別的地方都到處平滑.
令 D 為
 中的區域,
中的區域,
 為定義於
為定義於  的
的
 值函數.
再設
值函數.
再設
![$C: x=\gamma(t), t \in [a, b]$](img9.gif) 為 D 中的
piecewise smooth curve. 則線積分
(line integral, curvilinear integral)
為 D 中的
piecewise smooth curve. 則線積分
(line integral, curvilinear integral)
之定義為
C 叫做該線積分的積分路 (path of integration).
線積分的物理意義如下: 若一質點在力場 f(x)
之影響下沿曲線 C 移動, 則其行經 C 後位能的變化便是
線積分的定義和曲線 C 的參數 t 的選擇並無關係. 事實上若
![$h: [\alpha, \beta] \to [a, b]$](img13.gif) 為可微增函數,
為可微增函數,
 ,
則
,
則
通常幾何上所說的曲線, 未必附帶就給出了參數. 依這裡的討論,
只要曲線的方向確定, 無論怎麼選參數, 得到的線積分都一樣.
所以我們也可以認定線積分的積分路只是業已選定方向的幾何曲線,
其參數可以任選.
例 1
在平面上考慮
C1,
C2 二線如下:
C1 為連接 (0, 0)
和 (1, 1) 的直線線段, 即
C2 為連接 (0, 0) 至 (1, 0), 再連接 (1, 0) 至 (1, 1) 的折線:
則
但另一方面我們有
在前面的兩個積分裡, 線積分的值不但和積分路的端點有關,
並且和整條積分路 C 都有關, 而在後面的兩個例子裡兩個積分值是一樣的.
下定理指出線積分僅和 C 的端點有關的條件.

證明. First assmume that
 Then for every curve
Then for every curve
joing p to q we have
Conversely assume that the integral depends only on the end-points.
We fix a point
 For any point
For any point  define
define
where C is any path in D joining p0 to p. This function
F is well-defined because the integral is independent of path.
Let
and let C0 be the curve
Then by th mean-value theorem,
where  (0, 1). Letting
(0, 1). Letting  ,
we get
,
we get
Q. E. D
在本定理中所討論呈  形的函數, 叫作梯度場
(gradient field). 梯度場和以前講過的全微分有密切的關係:
若
形的函數, 叫作梯度場
(gradient field). 梯度場和以前講過的全微分有密切的關係:
若
 為
為
 中的梯度場, 則
中的梯度場, 則
在上面例1中,
 確是一個正合積分, 因為
確是一個正合積分, 因為
由本定理的前半段證明可知, 若 C 為連接 p 至 q 的
piecewise continuously differentiable curve 則
下定理是梯度場的一個必要條件:

這定理本身是一個 trivial 的結果.
H. Poincaré
問這定理的逆定理是否成立. 結果他得知逆定理之成立與否,
即上式是否保證 f 為梯度場,
和 D 的拓樸性質有關--即充要條件是 D 為 simply connected.
這是拓樸學的濫觴.
以下討論線積分的變數變換. 令 D 和 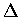 為
為
 中的兩個區域,
中的兩個區域,
為自 D 至 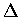 的映像. 我們假定每個
的映像. 我們假定每個  都連續可微.
又令
都連續可微.
又令
描寫 D 中的一條 piecewise continuously differentiable 曲線 C.
這曲線經  映成
映成 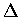 中的一條曲線
中的一條曲線  :
:
再設
 為
為 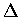 上的
上的
 值的連續函數. 考慮線積分
值的連續函數. 考慮線積分
因
 ,
故
,
故
從而
令
則有
這便是線積分變數變換的公式.
In addition to these line integrals, integrals with respect to
the arc length are also of importance. Thus, assume that F(x) is
a function defined for x varying in a domain
 ,
and that
,
and that
![$x=\gamma(t), t \in [a, b]$](img60.gif) ,
is a piecewise continuously
differentiable curve C in D. We denote by s(t) the arc length
of the curve C from
,
is a piecewise continuously
differentiable curve C in D. We denote by s(t) the arc length
of the curve C from  to
to  .
Then the line
integral of F with respect to the arc length is defined as
.
Then the line
integral of F with respect to the arc length is defined as
Note that in this discussion we only need F to be defined and
continuous on C. The previous type of line integrals may be
expressed in terms of the line integral introduced here. Thus, let
f(x) be an
 function in D, and let T(t) be the
unit vector tangent to C at
function in D, and let T(t) be the
unit vector tangent to C at  .
Then
.
Then
習

題
- 1.
- Let C be the unit circle in the plane. Evaluate
- 2.
- (a)
- Compute
 ,
where C is the square with vertices
,
where C is the square with vertices
 traversed
counterclockwise.
traversed
counterclockwise.
- (b)
- Evaluate the line integral
where C is the ellipse
4x2+y2=4 traversed counterclockwise.
- 3.
- Evaluate the line integral
where C is the ellipse
4x2+y2=4, traversed counterclockwise.
- 4.
- Compute
 where C is the curve
where C is the curve
![$x=t, y=t, z=t, t\in [0, 1]. $](img72.gif)
- 5.
- (a)
- Compute
 where C is the ellipse
2x2+y2=1 traversed counterclockwise.
where C is the ellipse
2x2+y2=1 traversed counterclockwise.
- (b)
- Let
f(x, y)=(y2, 0). Prove that f is not a gradient
field.
Note. f is a gradient field if
 such that
such that
 .
.
- 6.
- 用 C 表示擺線
 在
在
 中的一段. 試求關於弧長的線積分
中的一段. 試求關於弧長的線積分
 的值.
的值.
- 7.
- 設
f(x, y)=(x/(x2+y2), y/(x2+y2)), 其中
 .
.
- (a)
- 試證 f(x, y) 為一 gradient field.
- (b)
- 設曲線 C 之起點為 (1, 0), 終點為 (-2, 3),
其方程式為
y=x3+2x2-2x-1.
求線積分

Remark. The function F(x, y)such that
 in Exercise 7 is called the
logarithmic potential.
in Exercise 7 is called the
logarithmic potential.
- 8.
- Prove that the
 -valued function
-valued function
is a gradient field. Find a function
F(x, y, z) such that
Remark, The function
F(x, y, z)such that
 in Exercise 8 is called the
Newtonian potential.
in Exercise 8 is called the
Newtonian potential.
- 9.
- Show that
 is not an exact differential.
But if
is not an exact differential.
But if
then
is an exact differential.
Remark. The function f(x, y)in Exercise 9 is called an integrating factor. We shall study some
integrating factors in the Chapter7 of Part II of this course.



Next: 二變數函數的重積分
Up: 線積分與重積分
Previous: 線積分與重積分
1999-06-28
![]() ,
,
![]() 為
為
![]() 中的連續曲線,
若有
中的連續曲線,
若有
![]() 使
使 ![]() 局限在每個 [
ti-1, ti]
中時均有連續的導函數, (但當我們把
局限在每個 [
ti-1, ti]
中時均有連續的導函數, (但當我們把 ![]() 看成整個
[a, b] 上的函數時, 不要求
看成整個
[a, b] 上的函數時, 不要求
![]() ,
存在), 則稱 C 為
,
存在), 則稱 C 為
![]() 中的一條
piecewise continuously differentiable curve 或
piecewise smooth curve.
直觀地講,
piecewise smooth curve 是說這曲線除了在有限個點處可能轉硬灣外,
別的地方都到處平滑.
中的一條
piecewise continuously differentiable curve 或
piecewise smooth curve.
直觀地講,
piecewise smooth curve 是說這曲線除了在有限個點處可能轉硬灣外,
別的地方都到處平滑.
![]() 中的區域,
中的區域,
![]() 為定義於
為定義於 ![]() 的
的
![]() 值函數.
再設
值函數.
再設
![]() 為 D 中的
piecewise smooth curve. 則線積分
(line integral, curvilinear integral)
為 D 中的
piecewise smooth curve. 則線積分
(line integral, curvilinear integral)



![]() 為可微增函數,
為可微增函數,
![]() ,
則
,
則


![\begin{displaymath}\left\{ \begin{array}{ll}
x=1+t, \\
y=0,
\end{array} \right.
\ t \in [-1, 0],
\end{displaymath}](img18.gif)
![\begin{displaymath}\left\{ \begin{array}{ll}
x=1, \\
y=t,
\end{array} \right.
t \in [0, 1].
\end{displaymath}](img19.gif)





![]() Then for every curve
Then for every curve

![]() For any point
For any point ![]() define
define

![\begin{eqnarray*}\lefteqn{\frac{1}{h}[F(q)-F(p)]=\frac{1}{h}\int_{c_{0}} f(x) \c...
..._n)h\,dt\\
&=& f_{k}(x_1, x_2, \cdots, x_{k}+rh, \cdots, x_{n})
\end{eqnarray*}](img34.gif)
![]() 形的函數, 叫作梯度場
(gradient field). 梯度場和以前講過的全微分有密切的關係:
若
形的函數, 叫作梯度場
(gradient field). 梯度場和以前講過的全微分有密切的關係:
若
![]() 為
為
![]() 中的梯度場, 則
中的梯度場, 則



![]() 為
為
![]() 中的兩個區域,
中的兩個區域,





![]() ,
and that
,
and that
![]() ,
is a piecewise continuously
differentiable curve C in D. We denote by s(t) the arc length
of the curve C from
,
is a piecewise continuously
differentiable curve C in D. We denote by s(t) the arc length
of the curve C from ![]() to
to ![]() .
Then the line
integral of F with respect to the arc length is defined as
.
Then the line
integral of F with respect to the arc length is defined as



 ,
where C is the square with vertices
,
where C is the square with vertices


 where C is the curve
where C is the curve
 的值.
的值.
