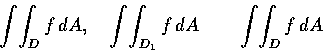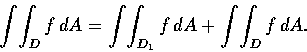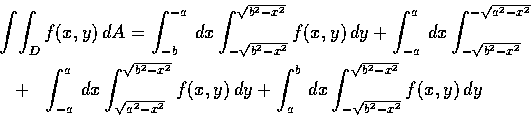Next: Green 定理
Up: 線積分與重積分
Previous: 線積分
把積分的觀念推廣到多變數的函數上去,
有很多種方向.
除了上面所說的線積分外,
最基礎的推廣便是多重積分 (multiple integral) 了.
但多重積分的計算有賴於疊積分 (itrated integral).
所以以下我們也討論2或3變數的函數的疊積分.
單變數函數積分的觀念由面積引發.
同樣地,
二變數函數積分的觀念可由體積引發.
我們希望能用嚴格的方法定義兩個變數函數的重積分
(或譯作二重積分 double integarl),
使合於下述的描述:
設兩個變數函數 f(x,y) 定義於區域
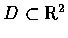 上.
在空間引入座標後,
把 D 看成 xy 平面中的集合,
則曲面 z=F(x,y) 和 D 間所夾的體積,
如果我們把其在 xy 平面以上的部份看成正的,
以下的部分看成負的,
便是 f(x,y) 在 D 上的重積分, 以
上.
在空間引入座標後,
把 D 看成 xy 平面中的集合,
則曲面 z=F(x,y) 和 D 間所夾的體積,
如果我們把其在 xy 平面以上的部份看成正的,
以下的部分看成負的,
便是 f(x,y) 在 D 上的重積分, 以
表之.
以上的討論不是重積分的定義, 而是一種直觀的解釋.
事實上從本節開始至下章末止, 我們不要求理論的嚴謹性,
而僅依靠直觀. 因為多變數函數的積分學應屬高等微積分的範圍,
此時無法講得嚴謹. 藉著直觀的解釋,
我們猜想重積分具下述諸性質:
(1) 若 c 為常數, 則
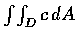 之值為 D 的面積的 c 倍.
之值為 D 的面積的 c 倍.
(2) 若 f, g 都在 D 上可積, a, b 都是常數,
則 af+bg 亦在 D 上可積, 且
(3) 若 f 在 D 上可積, 且 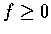 .
則
.
則
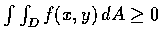 .
.
(4) 設
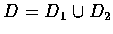 ,
D1, D2的交集是有限條線段的union, 則
,
D1, D2的交集是有限條線段的union, 則
三個重積分中只要有兩個存在, 第三個也存在, 且
例 2
設
D 為以原點為中心, 以
a 及
b 為半徑 (
a<
b)之二圓所夾的
環狀區域 (annulus),
f 為
D 上的可積分函數.
則將
D 分為四部分可得
1999-06-28
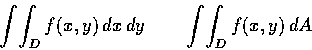
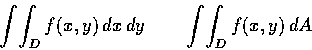
![]() 之值為 D 的面積的 c 倍.
之值為 D 的面積的 c 倍.
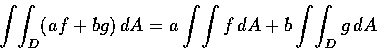
![]() .
則
.
則
![]() .
.
![]() ,
D1, D2的交集是有限條線段的union, 則
,
D1, D2的交集是有限條線段的union, 則