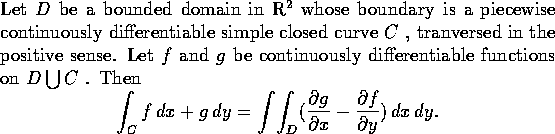
設 C 為 R2 中的一條 simple closed curve. 當我們依 t 增加的方向沿 C 繞行一週時, 若曲線的內部始終在我們的左側, 我們便說 C 是依正方向繞行的, 否則便說 C 是依負方向繞行的. 如果座標軸的選擇使 x 軸向右, y 軸向上, 則繞行的正方向便是逆時鐘方向.
英國數學家 George Green (1793--1841) 提出連繫線積分和重積分的一個定理, 其敘述如下:
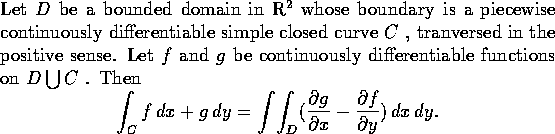
本定理的一般證明和 C 與 D 的幾何性質有關,
所以至少要等到高等微積分課程中纔可詳論.
以下我們僅就幾個特殊情形加以證明:
(1) 設
![]() 和
和
![]() 為 piecewise continuously
differentiable curves, 且對一切 x 均有
為 piecewise continuously
differentiable curves, 且對一切 x 均有
![]() .
設
.
設
C1:
![]() ,
動點從左端點移至右端點.
,
動點從左端點移至右端點.
C2: 連接
![]() 至
至
![]() 之線段.
之線段.
C3:
![]() ,
但依從右端點至左端點之方向.
,
但依從右端點至左端點之方向.
C4: 連接
![]() 至
至
![]() 之線段.
遂有
之線段.
遂有
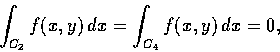
![\begin{displaymath}\int_{C_2} f(x, y)\,dx+\int_{C_3} f(x, y)\,dx=\int_a^b \displaystyle[f(x, \phi (x))-f(x, \psi (x))\displaystyle]\,dx
\end{displaymath}](img112.gif)
![\begin{displaymath}=-\int_a^b\left[\int_{\phi (x)}^{\psi (x)} \frac{\partial f}{...
...ght]\,dx=-\int\!\int_D \frac{\partial f}{\partial y}\,dx\,dy.
\end{displaymath}](img113.gif)
(2) 設
![]() 和
和
![]() 為 piecewise continuously
differentiable curve, 且對一切 y 均有
為 piecewise continuously
differentiable curve, 且對一切 y 均有
![]() .
設
.
設
(3) 設 D 可分割為有限部份:
![]() ,
其中任意兩部份的交界均在邊界上, 且每個 Di 均為第一款中的形式;
又設 D 也可分割為有限部份:
,
其中任意兩部份的交界均在邊界上, 且每個 Di 均為第一款中的形式;
又設 D 也可分割為有限部份:
![]() ,
其中任意兩部份的交界均在邊界上, 且每個 Ei 均為第二款中的形式,
則 Green 定理對 D 亦成立.
,
其中任意兩部份的交界均在邊界上, 且每個 Ei 均為第二款中的形式,
則 Green 定理對 D 亦成立.
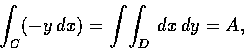
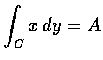 .
.