八八學年機械一B微積分課程 ◆
第 9 講
到目前為止,我們應該已經瞭解微分和積分個別的根本意義。
那些意義 (用數學極限所做的定義) 才是本。
而求導數的計算問題,本來是極需技巧或苦功的工作,
但是對於基本函數而言,卻有相當豐富的公式 (formula) 和規律 (rules)
來幫助我們運算,進而大量降低求導數的困難度。
我們倒也不能說,這些代數公式是末。
但是,如果只顧背公式和練習演算,而不去瞭解它們的原意,
那就真的可以說是本末倒置了。
之前我們從圖形、數值方面認識了微分。
現在,我們要從代數方面來認識它。
這一講的主題是
六個微分律與冪函數的導函數公式。
我們依以下順序,一面介紹微分律,一面推導公式。
以下,令 m、n 為正整數。
- xn 的導函數公式。這是最基本公式,Pascal
就已經知道了。輕易可以發現,當 n=0 的時候此形式的公式也成立。
- 線性律。應用在多項式的導函數性質。
- 乘法律。
- 反函數微分律。應用求出 x 開 n 次方根的導函數公式。
- 連鎖律 (Chain Rule)。應用求出 xn/m
的導函數公式。至此,發現 xr,只要 r
是正有理數,導函數公式形式上皆相同。
- 隱函數微分律 (derivatives for implicit functions)。
其實這只是連鎖律的一個應用。從這裡推導出來 1/x 的導函數公式。
- 除法律。其實這只是 (1/x)' 公式和連鎖律的一個應用。
- 最後,我們證明
(xr)' = r xr-1
這個微分公式對所有的有理數指數 r 都成立。
- 我們還沒有開始談無理數指數是什麼意義,所以就不去討論它的導函數公式了。
- 課本
- 4.1 4.2
請務必要閱讀課本內容,並且練習以下習題:
4.1: 4
4.2: 1--18 30 34 35 37 38 42 43
- 後記
- 今天沒有架設投影機,當然也沒有用遠距答題系統。因為資工的硬體還沒有來。
結果,提早 20 分鐘就講完了課,效率奇佳,有充裕的時間進行測驗。
- 小考題目
-
這次的測驗是將答案寫在紙上。其中第一題在課堂中有過明顯的暗示。
其他題目都是剛剛才講完的課題,而且同學們已經有些做導函數的技術底子,
不知道考試結果如何。
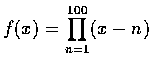 ,求
f ' (x)
,求
f ' (x)
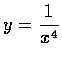 ,求 y '
,求 y '
 ,求 y '
,求 y '
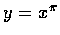 ,求 y '
,求 y '
- f(x)=x7 + 5x5
+4x3 - 6x -7,求
f(7)(x)。
- 求 y2=3x3+1 在 (1,2) 處之切線斜率。
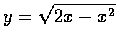 ,求 y '
,求 y '
- 滿分 10,應考 49 人,平均 8.2,標準差 1.76
回上層
Created: Oct 28, 1999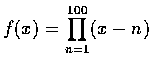 ,求
f ' (x)
,求
f ' (x)
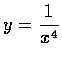 ,求 y '
,求 y '
 ,求 y '
,求 y '
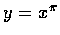 ,求 y '
,求 y '
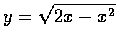 ,求 y '
,求 y '
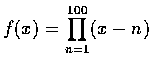 ,求
f ' (x)
,求
f ' (x)
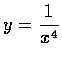 ,求 y '
,求 y '
 ,求 y '
,求 y '