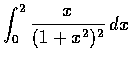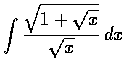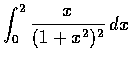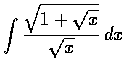八八學年機械一B微積分課程 ◆
第 15 講
今天的課題全部是補充教材。而且,就連我自己的講義都沒有完全準備好。
或者說,以前準備過,但是如今看來需要重寫。
所以,課堂筆記就相對顯得重要了。
其實我並無意要以較為抽象的數學內容來為難工學院一年級的學生。
我們的確可以認為,工學院學生不需要這些知識。
但是,太早斷言任何人不需要任何知識,永遠是危險的。
我們並不確知未來,如何能夠肯定任何一門知識的局限性呢?
站在數學這門學問的本位,身為一個數學老師的人,
似乎有責任交代一些真正數學的內容,而不只是充當傳授技藝的工具。
何況,沒有嘗試,怎麼能就此斷言學生沒有這個能耐?
引述項武義教授的話說:
如果將標準設得太低,大家反而一事無成。
現在,就好像在攀登的途中,我們暫時離開既定的路線,嘗試攀上一個小山峰。
雖我們無意進入那個深遠的山區,不過攀上去得以欣賞更深更遠的群山,
說不定對未來的旅程有些啟示或助益。
在我們開始之前,先預備一些邏輯基礎:
- 真值表,以 AND、OR、XOR、NOT 組成的邏輯語句,等價性
- 推論 (若 ... 則 ...)
- 充分 vs 必要條件
- 充分且必要 (若且惟若)
- 逆命題 (negation)
- 對偶命題 (counter positive)
- 全等命題 (equivalence)
- "for all" 和 "there exists" 以及它們的逆命題
在每一個課題上,我們會舉出一些例子。
- 課本
- 補充教材,課本中沒有對應內容
- 後記
- 轉眼間,一個月就過去了。我在上課後一個月來寫這個後記。
這一段時間的課,可以說是即興演出,事先沒有擬定腳本;
當然基本的目標是明確的。
事後發現,花整整兩堂課的時間來講邏輯,似乎恰好。
也許這種內容不該放在微積分課程裡面講,但是據我所知,
如果不趁著這時候交代給工學院同學,
則他們很可能再也沒有機會正式在課堂中認識這個課題。
而數理邏輯是所有人類理性活動的共同基礎,如果忽略了它,未免可惜。
這堂課的內容,以後要借機械系的錄影帶來補上講義。
- 小考題目
-
今天的考題來自前一講的習題。筆試,已經印製考卷。
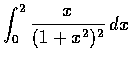
-
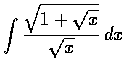



- 滿分 10,43 人應考,平均 3.0,標準差 1.95
回上層
Created: Nov 22, 1999