請務必要閱讀課本內容,並且練習以下習題:
8.1: 不必經過黎曼和,可直接寫出積分算式:1--3 7 9
8.2: 14 16 18 21 23
8.3: 1 4 6--8 10 14 15
- 定義珈瑪函數
(1) 求
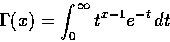

(2) 若 x > 0, 證明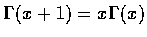
- 提出簡單解釋,判斷以下積分是否存在 (可積、有限)?不必算出答案。
- 滿分 10,44 人應考,平均 2.6,標準差 2.09。
今天照著課本講。這些是以前講過的教材,但是一直沒有留下中文講義。 這兩天的課題是:積分的應用。 其實這是個非常廣泛的課題,課本上提到的,最多只能說是: 積分應用的示範。
我們跳過黎曼和的部分,直接以非標準 (non-standard calculus) 的手法, 假想 x 的寬度 就是 dx。 如此來建立積分算式。並且現場用 Maple 工具軟體來求積分值。 今天講了一些幾何和物理類的應用問題。


