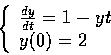八八學年機械一Ｂ微積分課程 ◆ 第 28 講

今天表面上沒有教新東西，仍然在課本 10.6 傅立葉級數的範圍內， 但是我添入了許多材料。

• 三角多項式
• 連續且能量有限的週期性函數的收斂理論
• 能量有限、只有有限多點不連續， 但不連續點的左右極限均存在的週期性函數的收斂理論
• 與泰勒級數對比
  • 部分和：n 階多項式、n 次調和函數
  • 逼近：局部、全域
  • 在一段區間收斂到 0：全部收斂到 0、未必
  • 需要可微、只需要連續

接著，我們按照課本講了例子和頻譜。

課本

10.6
請務必要閱讀課本內容，並且練習以下習題：
10.6: 已經指定過了

後記

小考題目

事先印好考卷。

1. (4 分) 求 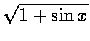以x=0 為參考點的前四個泰勒級數之非零項。
2. (2 分) 令 s 和 a 均為正值常數，而 當 R 很大的時候，已知
   
   求 A=?
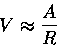
3. (2 分) 求以下微分方程在初始值附近的前四項級數解。
   
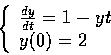
4. (2 分) 下列哪些是傅立葉級數？

   
   
   
   

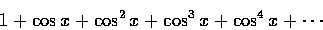
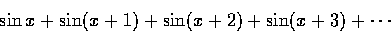
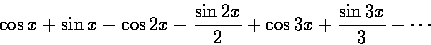
5. 滿分 10，43 人應考，平均 3.4，標準差 2.45。

回上層

• Back to the home page of Wei-Chang Shann.
• Connect to the home page of Department of Mathematics, National Central University, Taiwan.