八八學年機械一Ｂ微積分課程 ◆ 期末考

[考題]    [學習評量報告]

若非特別聲明，則所有變數均為實數，但 n 代表正整數。

1.
(30 points) 是非題。考慮以下各個敘述，如果您認為它是對的， 請在 □ 中打勾，否則請打叉。
□ 若 f(x) 在閉區間 [a,b] 內連續，且 $f(a)\cdot f(b)<0$， 則必有一 $c\in[a,b]$，使得 f(c)=0。
□ 若 f(x) 在閉區間 [a,b] 內連續，且存在某數 $c\in[a,b]$， 使得 f(c)=0，則必 $f(a)\cdot f(b)<0$。
□ 若 f(x) 在閉區間 [a,b] 內連續， 則必有一 $c\in[a,b]$，使得 $f(c)\cdot (b-a)=\int_a^b f(x)\,dx$
□ 若 f(x) 在區間 (a,b) 內可微， 在區間 [a,b] 內連續，而且 f(a) = f(b)， 則必有一 $c\in(a,b)$，使得 f '(c)=0。
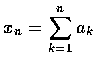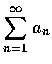□ 令 $x_n=\displaystyle\sum_{k=1}^n a_k$， 若 $\displaystyle\lim_{n\to\infty} x_n$ 收斂， 則 $\displaystyle\sum_{n=1}^\infty a_n$ 也收斂。
□ 若 f(x) 在 x=c 處連續，且 $\lim\limits_{n\to\infty} x_n = c$， 則 $\lim\limits_{n\to\infty} f(x_n) = f(c)$。
□ 若 xn 是一個數列，而且 $\lim\limits_{n\to\infty} x_n = c$。 若 $\lim\limits_{n\to\infty} f(x_n) = f(c)$，則 f(x) 在 x=c 處連續。
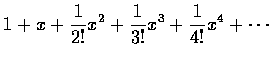□ 對任何實數 x， $\displaystyle 1+ x + {1\over 2!} x^2 + {1\over 3!}x^3 + {1\over 4!}x^4 + \cdots$ 必定收斂。
□ 對任何實數 x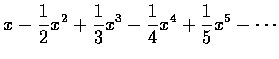， $\displaystyle x - {1\over 2} x^2 + {1\over 3}x^3 - {1\over 4}x^4 + {1\over 5}x^5 -\cdots$ 必定收斂。
□ $\displaystyle\sum_{n=1}^\infty {1\over n}$ 收斂。
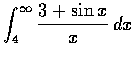□ 廣義積分 $\displaystyle\int_4^\infty {3+\sin x\over x}\,dx$ 是可積的。
□ 廣義積分 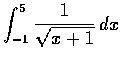$\displaystyle\int_{-1}^5 {1\over\sqrt{x+1}}\,dx$ 是可積的。
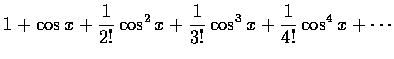□ $\displaystyle 1+\cos x+{1\over 2!}\cos^2x+{1\over 3!}\cos^3x +{1\over 4!}\cos^4x+\cdots$ 是一個傅立葉級數。
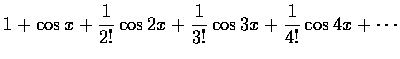□ $\displaystyle 1+\cos x+{1\over 2!}\cos2x+{1\over 3!}\cos3x +{1\over 4!}\cos4x+\cdots$ 是一個傅立葉級數。
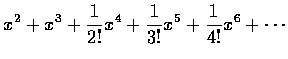□ x2ex2 以 x=0 為參考 點的泰勒級數是 $\displaystyle x^2+ x^3 + {1\over 2!} x^4 + {1\over 3!}x^5 +{1\over 4!}x^6 + \cdots$。
2.
(10 points) 求以下導函數：
\begin{displaymath}\hbox{(1) } {d\over dx}\int_0^x {t^4\over 4!}e^{-t}\,dt \qquad \hbox{(2) } {d\over dx}\int_0^{4x} {t^4\over 4!}e^{-t}\,dt \end{displaymath}

3.
(10 points) 假設當車速 v 介於 40 到 100 km/h 時， 汽車的耗油率是 $8+{1\over30}v$ km/$\ell$。若您的車速是
\begin{displaymath}v(t) = 80{t\over t+1}\quad\hbox{(km/h)} \end{displaymath}

請問在第二小時到第三小時的一小時內，共消耗幾公升的汽油？
4.
(15 points) 令 f(x) 是一個連續的 $2\pi$ 週期函數，它在一段週期內的定義是
\begin{displaymath}f(x) = \vert x\vert,\qquad x\in[-\pi,\pi) \end{displaymath}

請寫出它的傅立葉級數到 $\cos 4x$ 項，其中的係數寫到小數點下第四位。
5.
(15 points) 令 v 是氧分子在室溫下的速度，以 m/sec 為單位。 在為數非常多的氧分子中，各個速度不同。 麥斯威爾 (Maxwell) 認為這些分子的速度分佈函數 (distribution function) 是
\begin{displaymath}p(v) = a v^2 e^{-mv^2/(2kT)},\quad v\geq 0 \end{displaymath}

其中 $k=1.4\times 10^{-23}$ 是波茲曼 (Boltzmann) 常數， T 是凱氏溫標 (所謂室溫就是 $293^\circ K$)， $m=5\times 10^{-26}$kg 是氧分子的質量。試問
  1. a 的值大約是多少？寫出四位有效數字。
  2. 室溫中氧分子的平均速度大約是多少？寫出四位有效數字。
  3. p(v) 的最大值大約是多少？寫出四位有效數字。
6.
(20 points) 美國從 1790 到 1990 年間每十年一度的人口普查， 所顯示的美國總人口數如下表 (單位是百萬人)。
Year Population Year Population Year Population
1790 3.9 1860 31.4 1930 122.8
1800 5.3 1870 38.6 1940 131.7
1810 7.2 1880 50.2 1950 150.7
1820 9.6 1890 62.9 1960 179.0
1830 12.9 1900 76.0 1970 205.0
1840 17.1 1910 92.0 1980 226.5
1850 23.1 1920 105.7 1990 248.7
請以年份 t 為橫軸，t 從 1790 算起 (也就是說 t=0 代表 1790 年)； 人口成長率為縱軸，也就是說，要根據上表估計以下數值：
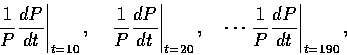
\begin{displaymath}\left. {1\over P}{dP\over dt}\right\vert _{t=10},\quad \left.... ...\cdots \left. {1\over P}{dP\over dt}\right\vert _{t=190},\quad \end{displaymath}

然後將這些點值畫在坐標平面上，發現它們大約落在一條直線上。 假設那條直線的方程式是 a-bt，請作以下問題。
  1. 根據上面的觀察，您就有了一個人口成長率的微分方程模型

    \begin{displaymath}{1\over P}{dP\over dt} = a-bt, \quad P(0)=3.9 \end{displaymath}

    根據這個微分方程，把 a、b 視為未知參數， 何時 (西元幾年) P(t) 將出現極大值？ (提示：極大值發生時，P'(t) 會怎樣？)
  2. 解上述微分方程。
  3. 請問您如何估計以下數值？照您的辦法估計其值到三位有效數字。

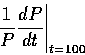
    \begin{displaymath}\left. {1\over P}{dP\over dt}\right\vert _{t=100} \end{displaymath}

  4. 請設計一個辦法來估計上述的 a 和 b。 並代入 (2) 中求得的解函數 P(t)。 按照這個模型，您預測美國今年將實施的人口普查，大約會有多少人口？ 而根據這個模型所預測的美國人口數之極大值是多少？

回上層

Created: Jan 13, 2000BR> Last Revised: Jan 13, 2000
© Copyright 2000 Wei-Chang Shann 單維彰

shann@math.ncu.edu.tw