八八學年機械一Ｂ微積分課程 ◆ 期中考

若非特別聲明，則所有變數均為實數，但 n 代表正整數。

1.

(30 points)是非題。考慮以下各個敘述，如果您認為它是對的，請在 □ 中打勾，否則請打叉。
□ 令 f(x)=x³+1，則 f(x) 有反函數。
□ 若 f(x) 在區間 (a,b) 內可微，則 f(x) 在 (a,b) 內有反函數。
□ 若 f(x) 在閉區間 [a,b] 內連續，且 $f(a)\cdot f(b)<0$ ，則必有一 $c\in[a,b]$ ，使得 f(c)=0。
□ 若 f(x) 在閉區間 [a,b] 內連續，且存在某數 $c\in[a,b]$ ，使得 f(c)=0，則必 $f(a)\cdot f(b)<0$ 。
□ 若 f(x) 在閉區間 [a,b] 內連續，則必有一 $c\in[a,b]$ ，使得 $f(c)\cdot (b-a)=\int_a^b f(x)\,dx$
□ 若 f(x) 在區間 (a,b) 內可微，在區間 [a,b] 內連續，而且 f(a) = f(b)，則必有一 $c\in(a,b)$ ，使得 f'(c)=0。
□ 若 $\displaystyle\lim_{n\to\infty} x_{2n} = L$ 且 $\displaystyle\lim_{n\to\infty} x_{2n+1} = L$ ，則必 $\displaystyle\lim_{n\to\infty} x_n = L$ 。
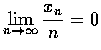□ 若 $\displaystyle\lim_{n\to\infty} x_n$ 收斂，則 $\displaystyle\lim_{n\to\infty} {x_n\over n}=0$ 。
□ 若 $0\leq x_n \leq y_n$ 且 $\displaystyle\lim_{n\to\infty} y_n=0$ ，則必 $\displaystyle\lim_{n\to\infty} x_n=0$ 。
□ 若 f(x) 在 x=c 處連續，且 $\lim\limits_{n\to\infty} x_n = c$ ，則 $\lim\limits_{n\to\infty} f(x_n) = f(c)$ 。

2.

(10 points) 若 y=f(x) 在 $x\in[0,2]$ 的函數圖形如下，試估計以下數值到小數點下一位。
$f'(1/2)\approx\qquad f'(1)\approx\qquad f'(3/2)\approx$

3.

(10 points) 令 $f(x)=\sin x$ 其中 x 以角度量為單位，亦即 $90^\circ$ 為一直角。求 f'(0)。

4.

(10 points) 陳述第一形式的微積分基本定理。並從它推導第二形式的微積分基本定理。

5.

(10 points) 令 $f(x)=e^{\sin x}$ ，請問
(1) 它是否為週期性函數？如果是，週期是多少？
(2) 它是否有垂直漸近線？
(3) 當 $x\to\pm\infty$ 時，f(x) 是否 $\to\pm\infty$ ？
(4) f(x)=0 是否有解？如果有，找出來。
(5) f(x) 是否有最小值？如果有，找出來。

6.

(10 points) 受空氣阻力的下落速度函數如下

$\begin{displaymath}v(t) = {mg\over k}\Bigl(1-e^{-{kt\over m}}\Bigr) \end{displaymath}$

其中 t 代表時間 (以秒為單位)、從落下的時刻算起， m 代表落體的質量 (以公斤為單位)， g=9.81，k 是某個正常數，而 v 的單位是公尺每秒。請問
(1) 落體的終極速度是多少？(亦即 $\lim\limits_{t\to\infty} v(t)$ )
(2) 若一名 60 公斤跳傘者的傘沒有打開，他在跳出飛機 10 秒後的速度達到 80% 的終極速度，求 k 是多少？
(3) 在上述情況下，這名可憐跳傘者的終極速度是每小時多少公里？

7.

(10 points) 若某產品的成本函數 (cost function) 是

C(q) = 0.3q³ -20q² +430q

其中 q 是生產數量。請問這個產品的固定成本 (fixed cost) 是多少？如果每個賣 230 元，可以全部賣掉，那麼產量多少的時候達到最高獲益 (maximum profit)？

8.

(10 points) 若 a>0， a(a²+1)y=a-x 是一條直線，稱之為 L。顯然可見 L 和 x 軸、y 軸在第一象限圍成一個三角形。當 a 是多少時，這個三角形的面積是 ${1\over5}$ ？當 a 是多少時，這個三角形的面積最大？

50 人應考，平均 62 分，標準差 9.7 分。
高於 73 的成績有 74 74 75 75 76 76 77 77 78 79 80
低於 53 的成績有 43 47 48 50 50 51 52

回上層

Back to the home page of Wei-Chang Shann.
Connect to the home page of Department of Mathematics, National Central University, Taiwan.

shann@math.ncu.edu.tw