Sum of 1 over n squared

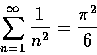
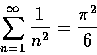
$\sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}6$

這是 Euler 在 1735 年發現的結果. 他的思路非常簡單, 當然也非常地巧妙. 現在我們就來欣賞 Euler 的推理過程.

考慮 $\frac{\sin x}{x}$ 這個函數, 它的零根出現在 $\pm n\pi$ 之處, 其中 n 是整數 ( $n\not=0$ ). 因此, 類似多項式的情況, 我們可以將 $\frac{\sin x}{x}$ 寫成以下的無窮乘積

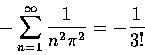
$\frac{\sin x}{x} = \prod_{n=1}^\infty \Bigl[1-\frac{x^2}{n^2\pi^2}\Bigr]$ 另一方面, $\frac{\sin x}{x}$ 以 0 為參考點的泰勒展開是 $frac{\sin x}{x} = 1 - \frac1{3!}x^2 + \frac1{5!}x^4 + \cdots$ 利用多項式的根與係數關係, 比較前面兩個式子中 x² 項的係數, 得到 $-\sum_{n=1}^\infty \frac1{n^2\pi^2} = -\frac1{3!}$ 稍作整理即是所求.

這種簡單的推理, 以今天的標準來看不無危險. 當然後來的數學家已經嚴格地證明了 Euler 的結果是對的. 但 Euler 也的確因為不嚴格而犯錯. 不論如何, 他將有限情況的事實推論到無限情況的巧妙手腕, 想必讓許多人感到驚奇與讚嘆.