本文轉介原載於 HPM 第 24 卷與第 25 卷的洪萬生老師文章。原文分為上、下兩篇，我將它們銜成一份 pdf 檔案，放在以下連結，方便讀者下載。
洪老師自己承認：
本文「從圭竇形談起」，意在吸引讀者眼球，我們的主要目標是《測量全義》的文本分析，特別是羅雅谷在撰著此書時，如何「收編」他所謂的「九章筭」（或中國傳統算書概念、算法及公式）。這篇文章確實跟「圭竇形」沒有很深的關聯，真正有意思的是洪老師對《測量全義》的解析與導讀。
我還是用一段話交代「圭竇形」吧。洪老師想要用「圭竇形」吸引讀者目光的意圖，未必有效。因為讀者恐怕都沒聽說過「圭竇形」也沒幾個人會因為這個名詞而想要打開文本來讀。其實「圭竇形」是「拋物線」第一次進入華語社會的名稱。這是《測量全義》的作者
— 羅雅谷 (Jacques Rho, 1593–1638) —
給 parabola 的中文譯名。「圭竇」是當時某些城門或宅邸大門旁邊開在牆上的洞口，用來收發文件或傳遞一些小東西，那樣的洞也許像戲院的票房 (box office)，上方是弧拱而下方是平臺，羅雅谷將它的邊框想像為開口向下的拋物線，當然這並不準確，絕不意味著當時牆上的「圭竇」是以二次曲線的概念製造的。當年的羅雅谷雖然具備新天文學的知識
— 他身為天主教神父，卻違背教宗旨意，不但偷偷閱讀哥白尼的日心說，還把《天體運行論》帶進中國 —
但是他應該還不知道伽利略發表的「自由拋射物之軌跡是 parabola」的理論，他還沒有「拋物軌跡」的概念。三民書局出版洪萬生老師的《數學故事讀說寫》，裡面有〈從圭竇形到拋物線：閒話數學名詞的翻譯語境〉。
p.3 出現 「叀術」及「綴術」，在馮立昇的《中國古代測量學史》也看到。馮立昇比較了《測量全義》、《測量法義》。
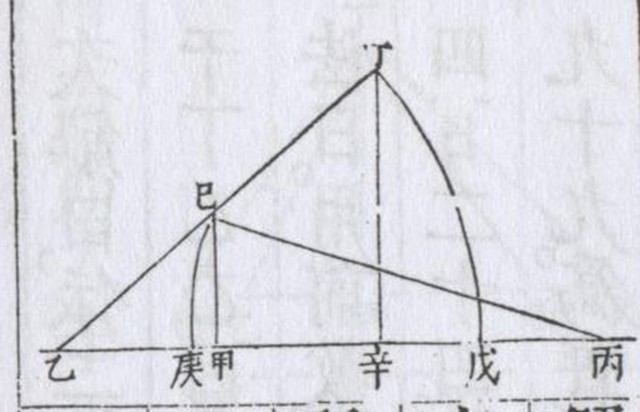
p.5 圖二是正弦定理的早年證明。羅雅谷負載《測量全義》裡的圖，其實是從約翰・穆勒 (Hohannes Müller, 1436–76) 的書裡複製出來的。示意的三角形是「巳乙丙」：
約翰・穆勒在明末有個很有趣的中文名字：「玉山若干」。我也查到另一個說法：「若玉山」。這個中文名字應該來自他的拉丁文名字 Ioannes de Monteregio，本來的意思是「來自山區的約翰」。拉丁名 Ioannes 現在一般譯為「約翰」，當時有譯為「若望」，也有「玉涵」。如今文獻中常見的約翰・穆勒拉丁名 Regiomontanus 是後來（1534 年）才被冠上的。費波那契也是類似的情況，Fibonacci 不是本名，是後來才被冠上這樣的稱呼。
p.7 羅雅谷沿用中國的「步」單位，但中國說面積時也用「步」，羅氏改說「方步」有創意。羅氏取一步 5 尺，一方步 25 方尺。
p.8 說〔先四邊形，後三角形〕「此一順序有違我們的直觀」。非也，羅雅谷在第九界說得清楚：正方形面積是所有面積的基礎，當然應該先談正方、長方，然後三角形的「面積」才有意義。
p.20
由於南宋版《九章算術》（含劉徽注）在明代失傳，因此，羅雅谷所謂的「九章筭」不可能指向《九章算術》，他當然更不可能知道劉徽的註解。同樣的情況，當然也適用於明末清初的中國數學家。梅文鼎就是一個絕佳的案例，他對劉徽注究竟有多少理解我們無從得知，儘管他曾看過《九章算術》第一卷〈方田章〉。〔注 15〕1678年，梅文鼎曾在黃虞稷處所見到《九章算術》方田章，但一生未見全書。參考李迪，《梅文鼎評傳》，頁429。
p.22
其中所涉「弧田」（弓形）也是「無法之形」，因此，羅雅谷顯然也不曾考慮這些圖形。看來「無法」就是「沒有公式」的意思。也許就是對於「公式」— 僅限有限多步驟的計算 — 的追求，限制了中國算家的想像力。
梅文鼎深受《測量全義》乃至《崇禎曆書》之影響，除了本文第五節所討論的具體案例之外，我們從他的年譜中，也可以找到文獻的證據。 其實，他的《平三角舉要》更是仿效《測量全義》之論述（體例），我們輕易複按即可掌握大致輪廓。史家劉鈍認為這是中國史上第一部三角學教程的著作，也是梅文鼎藉助中算勾股術整合（西方）三角學的一個嘗試。