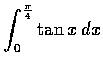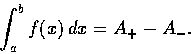
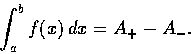
設
![]() ,
,
![]() ,
h>0, c, c+h 都在
[a,b] 內.
再令 M(h) 表 f 在 [c,c+h] 間的最大值,
m(h) 表 f 在 [c,c+h] 間的最小值.
則因
F(c+h)-F(c) 表示在 [c,c+h] 上 f 在 x 軸上部圖形的面積和在
x 軸下部圖形的面積的差, 所以有
,
h>0, c, c+h 都在
[a,b] 內.
再令 M(h) 表 f 在 [c,c+h] 間的最大值,
m(h) 表 f 在 [c,c+h] 間的最小值.
則因
F(c+h)-F(c) 表示在 [c,c+h] 上 f 在 x 軸上部圖形的面積和在
x 軸下部圖形的面積的差, 所以有
這個結論固然不錯, 但是它是在 (2) 的條件下導出來的. 條件 (2) 相當於 f 在 c 點連續. 又 f 在 c 和 c+h 間不一定會有最大值和最小值. 對這種 f, M(h) 和 m(h) 的選擇要修改. 不過對連續函數這些都不成問題.
把這個結論配合上均值定理 (見下章),
可得微積分的基分定理: 設 f 和 F 為 [a,b] 上的連續函數,
且對 ![]() ,
有
F'(x)=f(x), 則
,
有
F'(x)=f(x), 則
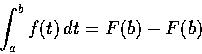
有關積分的一些基本公式, 高中都有介紹, 此處不贅. 積分除了求面積外, 還有不少應用. 茲舉二則其它應用如次:
A. 旋轉體 (surface of revolution) 的體積.
設 f(x) 為間隔 [a,b] 上的正值連續函數.
則直線 y=0, x=a, x=b 和曲線 y=f(x) 所圍成的區域繞 x軸旋轉所成的旋轉體的體積為
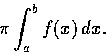
B. 功 (work) 的計算.
功的計算完全靠積分. 此處僅舉最簡單的情形如次: 設一質點在 x 軸上運動.
設它在點 x 處所受的力的水平分力為 f(x).
則當它從點 x=a 的位置移動到點 x=b 時, 所作的功為
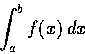
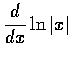 ,
(b)
,
(b)
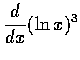 ,
(c)
,
(c)
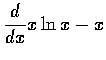 ,(d)
,(d)
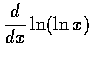 where x>1,
(e)
where x>1,
(e)
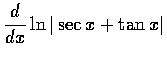 ,(f)
,(f)
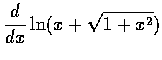 ,
(g)
,
(g)
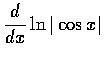 .
.
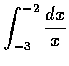 ,
(b)
,
(b)
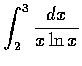 ,
(c)
,
(c)
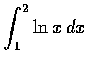 ,(d)
,(d)
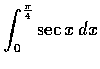 ,
(e)
,
(e)
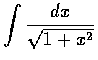 ,
(f)
,
(f)