


Next: About this document ...
Up: 數值方法
Previous: 積分的數值計算
Taylor (泰勒) 多項式可用來計算函數的近似值.
設 f(x) 在 c 點有 1 階、2 階乃至 n 階的導數,
則多項式
稱為 f(x) 在 c 點處的 Taylor 多項式.
在 c 點處 f(x) 和 Tn(x) 的值、它們的導數、二階導數、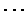 、
n 階導數的值均相等. 因此在 c 點附近,
Tn(x) 常常是 f(x) 的很好的近似值.
T1(x) 的圖形即 f(x) 在點 (c,f(c)) 的切線,
T2(x) 也是常常用得到的近似函數.
、
n 階導數的值均相等. 因此在 c 點附近,
Tn(x) 常常是 f(x) 的很好的近似值.
T1(x) 的圖形即 f(x) 在點 (c,f(c)) 的切線,
T2(x) 也是常常用得到的近似函數.
一切有關近似值得計算都應配合以誤差的討論,
以 Taylor 多項式做函數的近似值時的誤差, 叫做餘式, 將於下篇中詳論.
以上是高中微積分課程的大綱. 在我們的課程中這些都假定為已知.
習

題
- 1.
- 請判別下列各極限值是否存在, 若存在, 求其極限值.
(a)
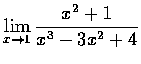 ,
(b)
,
(b)
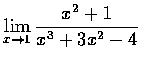 ,
(c)
,
(c)
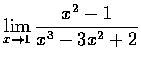 ,
,
(d)
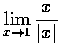 ,
(e)
,
(e)
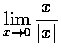 ,
(f)
,
(f)
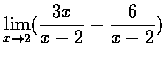 ,
,
(g)
![$\displaystyle\lim_{x\rightarrow2}[(\frac{1}{x}-\frac{1}{2})(\frac{1}{x-2})]$](img194.gif) ,
(h)
,
(h)
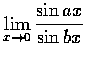 ,
式中
,
式中 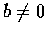 .
.
- 2.
- 設
請判別下列二極限值是否存在, 若存在, 求其極限值.
(a)
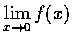 ,
(b)
,
(b)
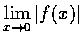 .
.
- 3.
- 令 A 為集合
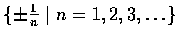 定義
定義
![$f:[-1,1]\longrightarrow\mathbb{R} $](img201.gif) 為
為
對任一
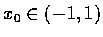 ,
問
,
問
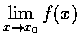 是否存在;
若存在, 求其極限值.
是否存在;
若存在, 求其極限值.
- 4.
- 令 A 如 3 題, 定義
對任一
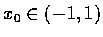 問
問
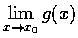 是否存在;
若存在, 求其極限值.
是否存在;
若存在, 求其極限值.
- 5.
- 定義
![$h:[-1,0) \cup (0,1] \rightarrow\mathbb{R} $](img207.gif) 如下:
當
如下:
當
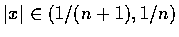 時,h(x) 之值定為 1/n,
若
時,h(x) 之值定為 1/n,
若
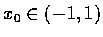 ,
問
,
問
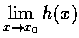 是否存在;
若存在, 求其極限值.
是否存在;
若存在, 求其極限值.
- 6.
- 定義
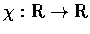 如下:
如下:
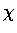 稱為有理數集合的特徵函數 (示性函數,
characteristic function 或 indicator function)
問哪些數 x0 可使
稱為有理數集合的特徵函數 (示性函數,
characteristic function 或 indicator function)
問哪些數 x0 可使
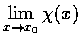 存在?
存在?
- 7.
- 試討論函數
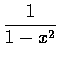 的單調性、
凹口方向及極值, 並繪出其圖形.
的單調性、
凹口方向及極值, 並繪出其圖形.
- 8.
- (a) 設 a, b 是給定的實數, 試證
(b) 設
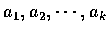 是實數, 試証
是實數, 試証
- 9.
- (a)設 m 為正整數, 則由微分公式
(xm)'=mxm-1 知
試利用極限的運算公式驗證這結果.
(b) 仿 (a) 利用例 3 及極限的運算公式驗證
(c) 設 m, n 為正整數, 試證
(d) 設 p, q, s, t 為正整數, 試證
- 10.
- 設 f, g 都是 n 次可微, 則 f(x)g(x) 亦 n 次可微, 且
註. 本公式稱為 Leibnitz rule.
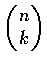 表示自 n 元素中選 k 元素的選法的個數.
表示自 n 元素中選 k 元素的選法的個數.
- 11.
- 當
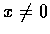 時設
時設
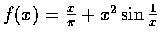 ,
又設 f(0)=0. 試証
,
又設 f(0)=0. 試証
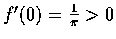 ,
但不可能有 s>0 使得 f 在 (-s,s) 間為增函數.
,
但不可能有 s>0 使得 f 在 (-s,s) 間為增函數.
提示. 設 k 為正整數,
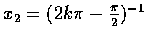 ,
,
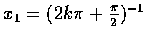 ,
則
x2>x1, 而
f(x2)<f(x1).
,
則
x2>x1, 而
f(x2)<f(x1).



Next: About this document ...
Up: 數值方法
Previous: 積分的數值計算
1999-06-27
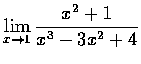 ,
(b)
,
(b)
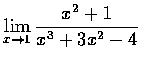 ,
(c)
,
(c)
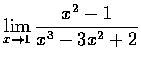 ,
,
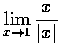 ,
(e)
,
(e)
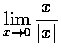 ,
(f)
,
(f)
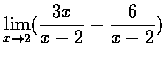 ,
,
![$\displaystyle\lim_{x\rightarrow2}[(\frac{1}{x}-\frac{1}{2})(\frac{1}{x-2})]$](img194.gif) ,
(h)
,
(h)
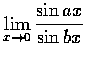 ,
式中
,
式中 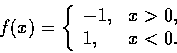
![\begin{displaymath}f(x)=\left\{
\begin{array}{ll}
10^{-100}, & \mbox{當 $x\in A$...
..., & \mbox{當 $x\in[-1,1]\setminus A$ 時}.
\end{array}
\right.
\end{displaymath}](img202.gif)
![\begin{displaymath}g(x)=\left\{
\begin{array}{ll}
\frac{1}{n}, & \mbox{當 $x=\fr...
... & \mbox{當 $x\in[-1,1]\setminus A$ 時}.
\end{array}
\right.
\end{displaymath}](img205.gif)
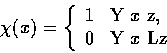
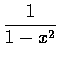 的單調性、
凹口方向及極值, 並繪出其圖形.
的單調性、
凹口方向及極值, 並繪出其圖形.
![\begin{displaymath}\lim_{x \rightarrow 1}\frac{\sqrt[m]{x}-1}{x-1}=\frac{1}{m}.
\end{displaymath}](img219.gif)
![\begin{displaymath}\lim_{x \rightarrow 1}\frac{\sqrt[m]{x}-1}{\sqrt[n]{x}-1}=\frac{n}{m}
\end{displaymath}](img220.gif)
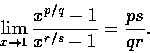
![\begin{displaymath}[f(x)g(x)]^{(n)}=\sum_{k=0}^{n}
\left(\!\!\begin{array}{c} n \\ k \end{array}\!\!\right)
f^{(k)}(x)g^{(n-k)}(x).
\end{displaymath}](img222.gif)